ว่าแต่เมทริกซ์คูณกันยังไง?

หากใครจำไม่ได้แล้วว่าการคูณเมทริกซ์นั้นทำอย่างไร เราจะย้อนเตือนความจำกันด้วยสมการนี้ สมมติว่าเมทริกซ์ $A$ มีขนาด $2 \times 3$ และเมทริกซ์ $B$ มีขนาด $3 \times 2$ พอนำมาคูณกันเมทริกซ์ผลคูณ $AB$ จะมีขนาด $2 \times 2$ 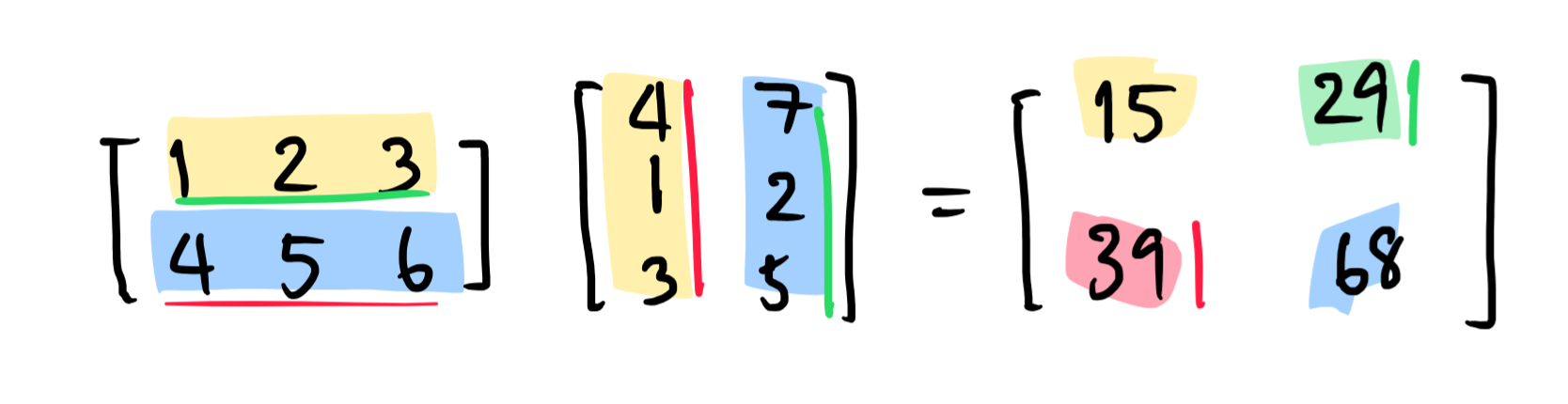จากภาพตัวอย่าง จำง่าย ๆ ว่าอันนี้เรียกว่าหลักคูณแถว แปลไทยเป็นไทยทับศัพท์ก็คือเอาคอลัมน์มาคูณกับแถว สมาชิกตัวสีเหลืองในด้านขวาเกิดจากผลคูณของแต่ละตัวในด้านซ้าย ดังนี้ $1\times 4 + 2 \times 1 + 3 \times 3 = 15$

ลองถอยจากตัวอย่างนี้ เมทริกซ์ใด ๆ สองตัว สมมติเรียกว่า $A$ และ $B$ จะคูณกันได้ก็ต่อเมื่อจำนวนหลักของเมทริกซ์ $A$ เท่ากับจำนวนแถวของเมทริกซ์ $B$ ขอสมมติว่าเท่ากันที่ $n$ (หลักสำหรับ $A$ แถวสำหรับ $B$) และผลลัพธ์ที่ได้จะมีขนาดเท่ากับจำนวนแถวของเมทริกซ์ $A$ และจำนวนหลักของเมทริกซ์ $B$ สมาชิกตำแหน่งที่ $ij$ (แถวที่ $i$ หลักที่ $j$) ของผลคูณ $AB$ จะเป็นไปตามสมการนี้ $$ AB_{ij}=\sum_{k=1}^n A_{ik} B_{kj} $$

ทำไมต้องทำให้ยากด้วย?

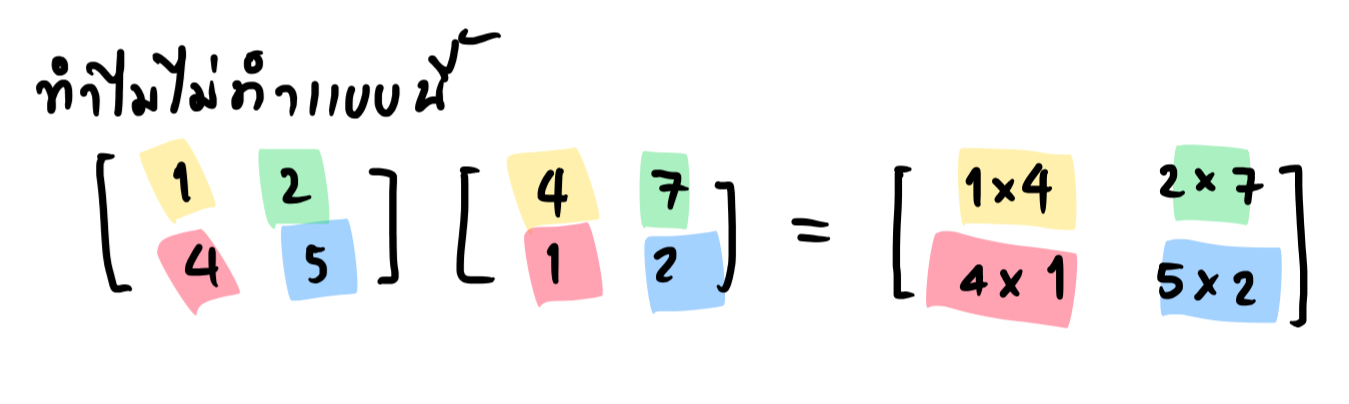คำถามตอนเรียนม.ปลายหรือมหาวิทยาลัย เชื่อว่าพอถึงเรื่องเมทริกซ์ ทุกคนน่าจะสงสัยว่าทำไมเมทริกซ์มันคูณกันแบบประหลาด ๆ แบบนี้ด้วย ทำไมไม่ทำให้ชีวิตเราง่าย ๆ ด้วยการนิยามให้ผลคูณของเมทริกซ์ เป็นผลคูณของแต่ละตัวเลย เช่นสมาชิกในหลักที่ 1 แถวที่ 1 ก็มาจากผลคูณของสมาชิกในตำแหน่งเดียวกันเท่านั้น ผมมีสามชุดของคำอธิบายที่ช่วยให้เข้าใจได้ว่าทำไมการคูณของเมทริกซ์จึงนิยามแบบนี้

คำอธิบายที่ 1: การแก้สมการเชิงเส้น

การนิยามผลคูณของเมทริกซ์แบบนี้ ทำให้เรามีวิธีการใหม่ในการแก้สมการเชิงเส้นที่เป็นระบบมากขึ้น สมมติว่าเรามีสมการเชิงเส้น 2 ตัวแปร 2 สมการ $$ \begin{cases} 2x - 4y = 9 \cr 4x + 2y = 1 \end{cases} $$ หากเราไม่รู้ว่าเมทริกซ์คืออะไร เราก็ยังสามารถแก้สมการนี้โดยตรง เริ่มจากเลือกหนึ่งสมการ จากนั้นค่อย ๆ จัดรูปตัวแปร $x$ (หรือ $y$) ให้อยู่ในรูปของอีกตัวแปรหนึ่ง $y$ (หรือ $x$) ในกรณีนี้สมการนี้ก็ไม่ได้ยากอะไร ทีนี้ถ้าเราอยากจะแก้ระบบสมการที่ใหญ่ขึ้นมาหน่อย เป็น 10 หรือ 100 ตัวแปรหละ เราจะทำอย่างไร หากจะนั่งจัดสมการให้อยู่ในรูปของตัวแปรอื่นและแทนค่าย้อนกลับเรื่อย ๆ ก็ย่อมทำได้ เพียงแค่จะวุ่นวายและยุ่งเหยิง ในเมื่อเรานิยามผลคูณของเมทริกซ์แล้ว เราสามารถแก้ระบบสมการเชิงเส้นได้โดยการเขียนเป็นเมทริกซ์ได้เลย

ระบบหลายสมการเปลี่ยนเป็น 1 สมการเมทริกซ์

ระบบสมการในตัวอย่างนี้สามารถแทนได้ด้วยสมการเมทริกซ์เพียงสมการเดียว

$$\begin{bmatrix}2 & -4 \\ 4 & 2\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix} 9 \\ 1\end{bmatrix}$$ การจะแก้สมการนี้ก็สามารถทำได้หลายวิธีเช่น การลดรูปให้เป็นรูปแบบขั้นบันได คำนวณเมทริกซ์อินเวิร์ส สมมติว่าเราคำนวณเมทริกซ์อินเวอร์สได้ $A^{-1}$ คำตอบของสมการ (ค่าของ $x$ และ $y$ ที่กำหนดโดยสมการนี้) ก็หาได้จากการคูณเมทริกซ์อินเวิร์สกับเมทริกซ์ในทางขวาของสมการ

ความพิเศษของการเขียนเช่นนี้คือเราสามารถรู้ได้ทันทีเลยกว่าระบบสมการนี้มีคำตอบกี่คำตอบ (หมายความว่าสมการมีค่า $x$ และ $y$ ได้ทั้งหมดกี่ค่า) ค่าที่เป็นตัวบอกว่าเราแก้สมการให้ได้ค่า $x$ และ $y$ เพียงคู่เดียวหรือไม่ก็คือค่าที่เรียกว่า ดีเทอร์มิเนนต์ (determinant) ของเมทริกซ์ $A$ ซึ่งในที่นี้คือ $2\times 2 - 4\times 4 = -12$

ระบบที่ใหญ่ขึ้นแต่เมทริกซ์เหมือนเดิม

ทีนี้ถ้าเรามีระบบสมการหลายตัวแปรหลายสมการที่ใหญ่ขึ้นมา แต่ก็ยังบรรยายได้ด้วยเมทริกซ์เดิม ก็สามารถแก้ได้เช่นเดียวกัน สมมติว่าเรามีระบบสมการเชิงเส้น 4 ตัวแปร 4 สมการ $$\begin{cases} 2x - 4y = 9 \cr 2w - 4z = 12 \cr 4x + 2y = 1 \cr 4w + 2z = 7 \end{cases}$$ แม้ว่าจะมี 4 ตัวแปร แต่ก็ความสัมพันธ์ระหว่างคู่ตัวแปรเหมือนเดิม (ความสัมพันธ์ระหว่าง $x$ กับ $y$ และ $w$ กับ $z$) เราก็จัดตัวแปรให้อยู่ในรูปของเมทริกซ์ได้เช่นเดียวกัน $$\begin{bmatrix}2 & -4 \\ 4 & 2\end{bmatrix}\begin{bmatrix}x & w\\ y & z\end{bmatrix}=\begin{bmatrix} 9&12 \\ 1&7\end{bmatrix}$$ คำตอบของสมการนี้ก็หาได้ด้วยวิธีเดิมคือคูณด้วยอินเวอร์สของเมทริกซ์ทางซ้ายสุดเข้าไปในสมการ เราจะได้คำตอบออกมา

ที่เราสามารถทำเช่นนี้ได้ ก็เป็นเพราะว่าการคูณเมทริกซ์ที่นิยามนี้อนุญาตให้เมทริกซ์ทางขวาของการคูณจะมีกี่หลักก็ได้ ขอเพียงให้มีจำนวนแถวเท่ากับจำนวนหลักของเมทริกซ์การคูณที่อยู่ทางขวา และตัวเลขที่อยู่ในแต่ละหลักของเมทริกซ์ทางขวามีความอิสระจากหลักอื่น ๆ

ระบบที่ใหญ่ขึ้นและซับซ้อนมากขึ้น

ถ้าเรามีระบบสมการหลายตัวแปรหลายสมการที่ใหญ่ขึ้นมา และมีความซับซ้อนมากขึ้น เช่น $$\begin{cases} w + x - 4y + 3z = 12 \cr 2x - 4y + 3z = 9 \cr 3w + 7x + 2y = 1 \cr 4w + 2x + 3z = 7 \end{cases}$$ เราก็ยังสามารถจัดเรียงตัวแปรพวกนี้ให้เข้าไปอยู่ในแบบเมทริกซ์ได้เช่นกัน $$\begin{bmatrix} 1& 1 & -4 & 3 \\ 0& 2 & -4 & 3 \\ 3& 7 & 2 & 0\\ 4 & 2 & 0 & 3 \end{bmatrix}\begin{bmatrix}w\\ x\\ y \\z \end{bmatrix}=\begin{bmatrix} 12 \\ 9 \\ 1 \\ 7 \end{bmatrix}$$ การคำนวณอินเวอร์สอาจจะยุ่งยากหน่อย แต่เราก็มีวิธีการคำนวณดีเทอร์มิเนนต์สำหรับเมทริกซ์ขนาดใหญ่ ๆ จากนิยามของดีเทอร์มิเนนต์สำหรับเมทริกซ์จตุรัส $A$ ขนาด $n\times n$ ก็คือ $$\mathrm{det}(A) = \sum_{i_1 i_2 i_3 … i_n}\mathrm{sign}(i_1 i_2 i_3 … i_n) A_{1i_1}A_{2i_2} … A_{ni_n}$$ สัญลักษณ์ $\mathrm{sign}()$ คือฟังก์ชันที่ให้ค่าเป็น $1$ หรือ $-1$ ซึ่งขึ้นอยู่กับการเรียงลำดับของตัวเลขที่อยู่ในวงเล็บ ถ้าเป็นลำดับที่เรียงลำดับ 1 ถึง $n$ จากน้อยไปมากจะให้ค่าเป็น $1$ เช่นถ้าเป็นลำดับ $123$ ก็จะให้ค่าเป็น $1$ แต่ถ้าสลับตำแหน่งกันเป็นจำนวนคี่ครั้งก็จะให้ค่าเป็น $-1$ เช่นลำดับ $132$ ก็จะให้ค่าเป็น $-1$ การนิยามแบบนี้สะดวกกับการเขียนโค้ดเพราะที่สิ่งนิยามนี้บอกคือให้คอมพิวเตอร์บวกเลขไปเรื่อย ๆ ให้ครบทุก ๆ การสลับเปลี่ยนที่ของลำดับที่เป็นไปได้

การหาอินเวอร์สของเมทริกซ์ขนาดใหญ่สามารถทำได้หลายวิธีที่ สำหรับผู้ที่สนใจสามารถเข้าไปดูได้ที่ลิงก์นี้

ถ้านิยามให้คูณง่าย ๆ จะไม่มีวิธีทำอะไรแบบนี้หรอ

ถ้าเรานิยามการคูณว่าเป็นผลคูณของแต่ละตัวเลย เมทริกซ์แต่ละตัวจะคูณกันได้ก็ต่อเมื่อขนาดของเมทริกซ์เท่ากัน ทั้งจำนวนแถวและทั้งจำนวนหลัก ดังนั้นทางเดียวที่จะเขียนสมการการได้ก็คือ $$\begin{bmatrix}2x -4y \\ 4x+2y\end{bmatrix}= \begin{bmatrix}9\\ 1\end{bmatrix}$$ ซึี่งไม่ได้ให้อะไรใหม่นอกจากประหยัดหมึกเขียนเครื่องหมายเท่ากับ

สรุปตอนที่ 1

การนิยามการคูณเมทริกซ์แบบนี้ช่วยให้เราแก้ระบบสมการได้อย่างเป็นระบบมากขึ้น

คำอธิบายที่ 2 ในตอนต่อไปจะพูดถึงการคูณเมทริกซ์ในบริบทที่กว้างกว่าการแก้ระบบสมการเชิงเส้น

อันนี้เป็นบทความแรก ถ้าใครมีอะไรสงสัยหรืออยากแนะนำอะไร สามารถแสดงความคิดเห็นได้ในเพจเฟสบุ๊ค “บล็อกของทกล้า”