หลาย ๆ คนตอนเรียนน่าจะเรียนมาว่าเมทริกซ์คือตัวเลขที่เรียงกันในตาราง และก็นิยามการบวกว่าเป็นการดำเนินการในแต่ละสมาชิกที่อยู่ในตำแหน่งเดียวกัน และนิยามการคูณว่าเป็นการนำแต่ละตัวในแถวไปคูณแต่ละตัวในหลัก คำถามที่ทุกคนน่าจะมีคือทำไมถึงนิยามเช่นนี้ มันมีความหมายอะไร เราได้ให้ตัวอย่างไปแล้วในสองบทความก่อนหน้า สำหรับบทความนี้ เราจะนำเสนอเมทริกซ์ในมุมมองที่เป็นนามธรรมมากขึ้น เพื่อให้เห็นคอนเซปของเมทริกซ์แบบที่ไม่ได้ติดพันอยู่กับแค่บริบทใดบริบทหนึ่ง อย่างไรก็ดีเรานำเสนอตัวอย่างด้วยว่าเมทริกซ์สามารถบรรยายการขายผักได้

การคูณเมทริกซ์กับเวกเตอร์ และฟังก์ชันเชิงเส้น

หนึ่งในวิธีที่จะเข้าใจเมทริกซ์คือการมองว่าเมทริกซ์เป็นการเขียนบรรยายฟังก์ชันเชิงเส้นหลายตัวแปรในรูปแบบหนึ่ง (ขอให้ทดไว้ในใจว่าจะเป็นฟังก์ชันตัวแปรเดียวก็ได้)

ฟังก์ชันเชิงเส้น

ฟังก์ชันเชิงเส้นหมายถึงฟังก์ชันประเภทที่มีหน้าตาเช่น $$f(x)=ax$$ โดยที่ $a$ เป็นค่าคงที่ และ $x$ เป็นตัวแปร ถ้ามีหลายตัวแปรก็จะเป็น $$f(x_1,x_2,\dots,x_n)=a_1x_1+a_2x_2+\dots+a_nx_n$$ โปรดระมัดระวังว่าสิ่งนี้ต่างจากการสมการเส้นตรงที่หน้าตาเป็น $$y=ax+b$$

เมื่อเราลองเทียบระหว่างการคูณเมทริกซ์กับการบรรยายฟังก์ชันเชิงเส้นตัวแปรเดียว เราจะเห็นว่าเราสามารถเขียนฟังก์ชันนี้ว่าเป็นการคูณระหว่างเมทริกซ์ขนาด $1\times n$ กับเมทริกซ์ขนาด $n\times 1$ ได้ $$f(x_1,x_2,\dots,x_n)=\begin{bmatrix}a_1&a_2&\dots&a_n\end{bmatrix}\begin{bmatrix}x_1\\x_2\\ \vdots\\ x_n\end{bmatrix}$$

หลายฟังก์ชันเชิงเส้น หลายตัวแปร

ทีนี้ถ้าเราลองขยายแนวคิดนี้ออกไป แทนที่เราจะเขียนฟังก์ชันเพียงฟังก์ชันเดียว เรามีหลาย ๆ ฟังก์ชัน เช่น $$f_1(x_1,x_2,\dots,x_n)=a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n$$ $$f_2(x_1,x_2,\dots,x_n)=a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n$$ $$\vdots$$ $$f_m(x_1,x_2,\dots,x_n)=a_{m1}x_1+a_{m2}x_2+\dots+a_{mn}x_n$$ เราสามารถเขียนเป็นเมทริกซ์ได้เช่นกัน $$\vec{f} = \begin{bmatrix}f_1(x_1,x_2,\dots,x_n)\\ f_2(x_1,x_2,\dots,x_n)\\ \vdots\\ f_m(x_1,x_2,\dots,x_n)\end{bmatrix}=\underbrace{\begin{bmatrix}a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}&a_{22}&\dots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&\dots&a_{mn}\end{bmatrix}}_{:= A}\begin{bmatrix}x_1\\ x_2\\ \vdots\\ x_n\end{bmatrix}$$ 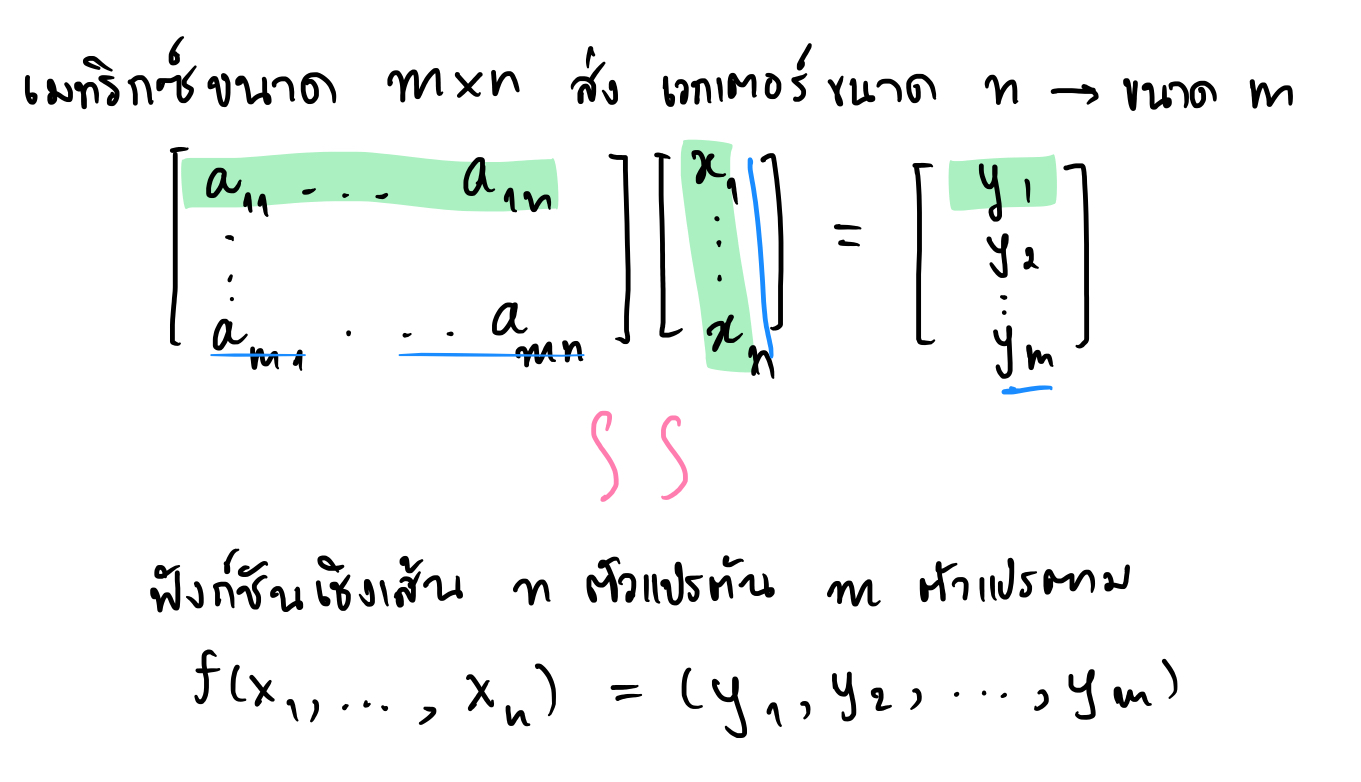นั่นก็คือการคูณเมทริกซ์ $A$ ขนาด $m\times n$ กับเวกเตอร์ขนาด $n$ (เมทริกซ์ขนาด $n\times 1$) สามารถมองได้ว่าคือการใส่ตัวแปรต้นจำนวน $n$ ตัว เข้าไปในฟังก์ชันเชิงเส้นจำนวน $m$ ฟังก์ชัน ผลลัพธ์ที่ได้ก็คือเวกเตอร์ของตัวแปรตามขนาด $m$ ตัว เราอาจจะพอจำเป็นสโลแกนได้ดังนี้

ใช้ขายผัก

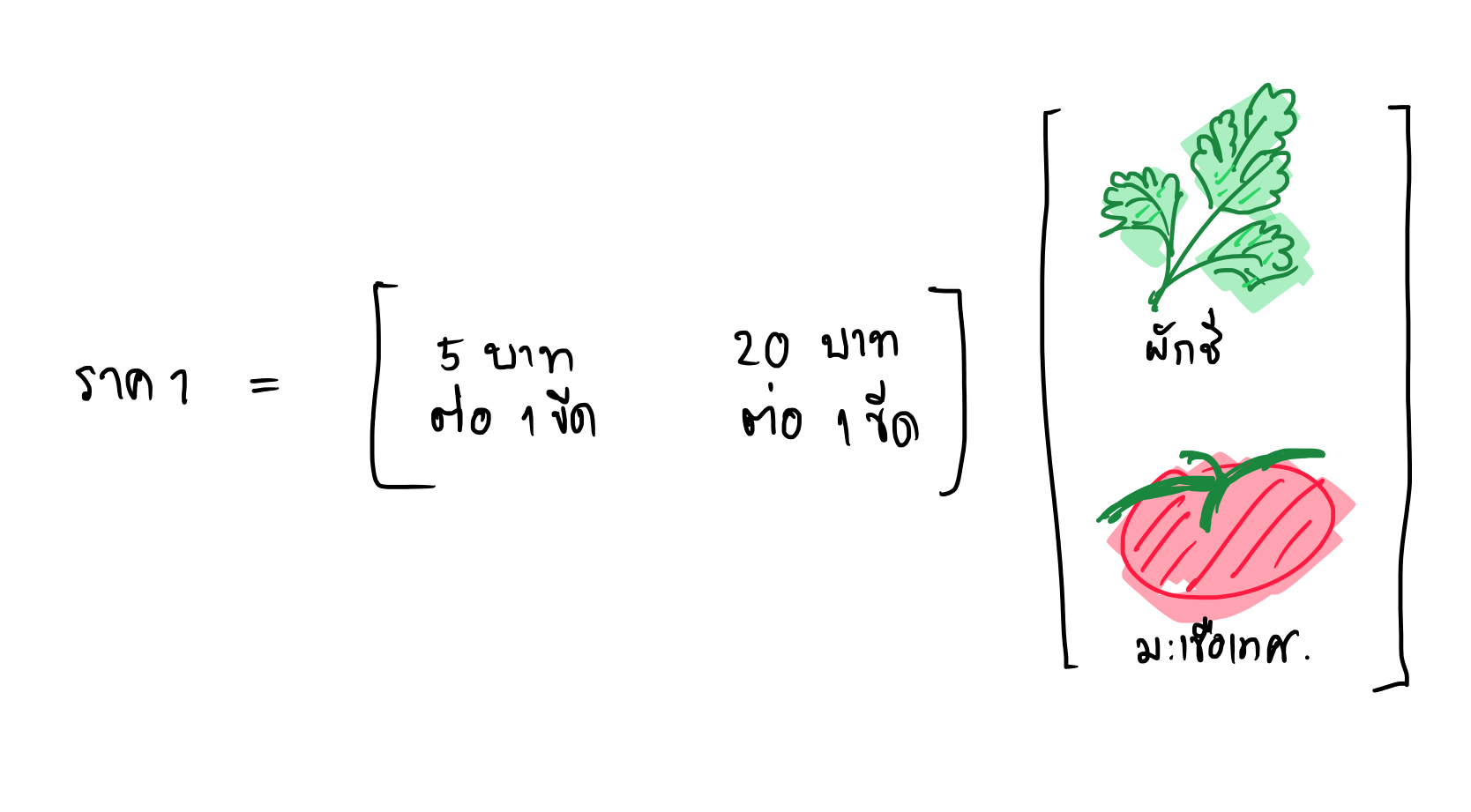
สมมติว่าเราเปิดร้านขายผัก แต่ร้านนี้เพิ่งเปิดเงินลงทุนยังไม่มาก เรามีผักขายแค่สองชนิดคือผักชีและมะเขือเทศ (มะเขือเทศจัดเป็นผักได้ เช่นเดียวกับพริก บวบ ฟัก หรือมะเขือ อ้างอิง)

แม้จะเปิดร้านได้ไม่นาน แต่ร้านก็ขายดี ทุก ๆ วันก็ขายหมด ดังนั้นเราสามารถที่จะบรรยายรายได้และต้นทุนของการขายผ่านฟังก์ชันที่มีตัวแปรต้นเป็นปริมาณของสินค้าที่เรามีในแต่ละวันได้เลย สมมติว่าเรามีฟังก์ชันเชิงเส้นที่บรรยายต้นทุนผันแปรของการผลิตสินค้า ($f(x_1,x_2)$) และรายได้จากการขาย ($g(x_1,x_2)$) เราให้ $x_1$ และ $x_2$ แทนน้ำหนัก/มวลในหน่วยขีดของผักชีและมะเขือเทศตามลำดับ

สมมติว่าต้นทุนผันแปรของการผลิตสินค้าผักชีคือ 2 บาทต่อ 1 ขีด และของมะเขือเทศคือ 10 บาทต่อ 1 ขีด เราตั้งราคาขายผักชีอยู่ที่ 5 บาทต่อขีด และราคาขายมะเขือเทศอยู่ที่ 20 บาทต่อขีด นั่นคือต้นทุนผันแปรจากการผลิตสินค้าสามารถเขียนเป็นเมทริกซ์ได้ ดังนี้ $$\begin{bmatrix}f(x_1,x_2)\end{bmatrix}=\begin{bmatrix}2&10\end{bmatrix}\begin{bmatrix}x_1\\ x_2\end{bmatrix} = 2x_1 + 10x_2$$

ส่วนรายได้จากการขายสินค้าสามารถเขียนเป็นเมทริกซ์ได้ดังนี้ $$\begin{bmatrix}g(x_1,x_2)\end{bmatrix}=\begin{bmatrix}5&20\end{bmatrix}\begin{bmatrix}x_1\\ x_2\end{bmatrix}$$

เมื่อเรามีฟังก์ชันเชิงเส้นสองฟังก์ชัน และต้องการหาผลตอบแบบเวกเตอร์ของฟังก์ชันเชิงเส้นทั้งสอง ก็สามารถทำได้โดยการคูณเมทริกซ์เช่นกัน $$\vec{f} := \begin{bmatrix}f(x_1,x_2)\\ g(x_1,x_2)\end{bmatrix}=\underbrace{\begin{bmatrix}2&10\\ 5&20\end{bmatrix}}_{:=F}\begin{bmatrix}x_1\\ x_2\end{bmatrix}$$

สำหรับเวลาเราคิดราคาขายผัก ก็ทำได้เช่นเดียวกันกับเวลาเราคำนวณรายได้จากการขายสินค้า

การคูณเมทริกซ์กับเมทริกซ์ และฟังก์ชันประกอบ

การนิยามการคูณเมทริกซ์ให้รูปแบบที่เป็นธรรมชาติในการบรรยายฟังก์ชันประกอบ (Composite function) ฟังก์ชันประกอบก็คือฟังก์ชันที่เกิดจากการทำต่อกันของฟังก์ชันมากกว่าหนึ่งฟังก์ชัน มักจะเขียนว่า $g\circ f$ หรือ $g(f(x))$ โดยที่ $f$ และ $g$ เป็นฟังก์ชัน

สำหรับการขายผัก ถ้าเราต้องการที่จะคำนวณกำไรจากการขาย (ขอเรียกว่า $h$) สิ่งที่เราทำคือการนำต้นทุน ($f$) มาลบจากราคาที่เราขายได้ ($g$) นั่นก็คือ $$h = -f + g$$ สังเกตว่า $h$ เป็นฟังก์ชันเชิงเส้น ที่มีตัวแปรต้นเป็น $f$ และ $g$ ซึ่งเป็นฟังก์ชันเชิงเส้นด้วย เราสามารถเขียน $h$ แทนด้วยเมทริกซ์ที่คูณกับเวกเตอร์ $(f,g)$ ได้ดังนี้ $$h=\underbrace{\begin{bmatrix}-1&1\end{bmatrix}}_{H} \begin{bmatrix}f(x_1,x_2)\\ g(x_1,x_2)\end{bmatrix}$$ เรารู้ว่าเวกเตอร์ของ $f$ และ $g$ เขียนได้ในรูปเมทริกซ์ $F$ คูณกับเวกเตอร์ของ $x_1$ และ $x_2$ ดังนั้นเราสามารถเขียน $h$ ให้อยู่ในรูปของเมทริกซ์คูณเมทริกซ์และคูณกับเวกเตอร์ได้ดังนี้ $$h=\begin{bmatrix}-1&1\end{bmatrix}\begin{bmatrix}2&10\\ 5&20\end{bmatrix}\begin{bmatrix}x_1\\ x_2\end{bmatrix}$$ ถึงตรงนี้ อยากให้ค่อย ๆ พิจารณาว่าเกิดอะไรขึ้น เรามองที่เมทริกซ์ $F$ และ $H$ ว่าเป็นฟังก์ชันเชิงเส้น $h$ ก็คือผลลัพธ์จากการใส่ $x_1$ และ $x_2$ ลงไปในฟังก์ชันเชิงเส้น $F$ และ $H$ ตามลำดับ นั่นคือ $$h= H\circ F (x_1, x_2)=H(F(x_1,x_2))$$ เรารู้ว่าเมทริกซ์มีสมบัติการเปลี่ยนกลุ่ม แทนที่เราจะคูณเมทริกซ์ $F$ กับเวกเตอร์ $(x_1,x_2)$ แล้วจึงคูณกับ $H$ เราสามารถคูณเมทริกซ์ $H$ กับเมทริกซ์ $F$ ก่อนได้เช่นกัน $$h= H(F\vec{x}) = (HF)\vec{x}$$ ดังนั้นเราสามารถเขียน $h$ ให้กระชับลงได้ดังนี้ $$h=\begin{bmatrix}-1&1\end{bmatrix}\begin{bmatrix}2&10\\ 5&20\end{bmatrix}\begin{bmatrix}x_1\\ x_2\end{bmatrix} = \begin{bmatrix}3&10\end{bmatrix}\begin{bmatrix}x_1\\ x_2\end{bmatrix}$$

กฏการคูณเมทริกซ์

การมองว่าเมทริกซ์คือสิ่งที่แสดงฟังก์ชันเชิงเส้นหลายตัวแปรต้นหลายตัวแปรตามให้ภาพที่ชัดเจนเกี่ยวกับเงื่อนไขว่าเมื่อใดที่เมทริกซ์จะคูณกันได้ เช่นการคูณเมทริกซ์ $BA$ จะทำได้ก็ต่อเมื่อจำนวนหลักของ $B$ มีค่าเท่ากับจำนวนแถวของ $A$ การให้เหตุผลจากมุมมองนี้เป็นดังต่อไปนี้

1. เมทริกซ์ A ให้ตัวแปรตาม (output) ออกมาเท่ากับจำนวนแถวของเมทริกซ์
2. เมทริกซ์ B ใช้ตัวแปรต้น (input) เท่ากับจำนวนหลักของเมทริกซ์
3. เมทริกซ์ BA แสดงถึงฟังก์ชันประกอบของเมทริกซ์ B และ A ฟังก์ชันจะประกอบกันได้ฟังก์ชัน A ต้องให้จำนวนตัวแปรตาม เท่ากับ จำนวนของตัวแปรต้นที่ B ต้องใช้

เราพอจะสรุปเป็นภาพได้ดังนี้ 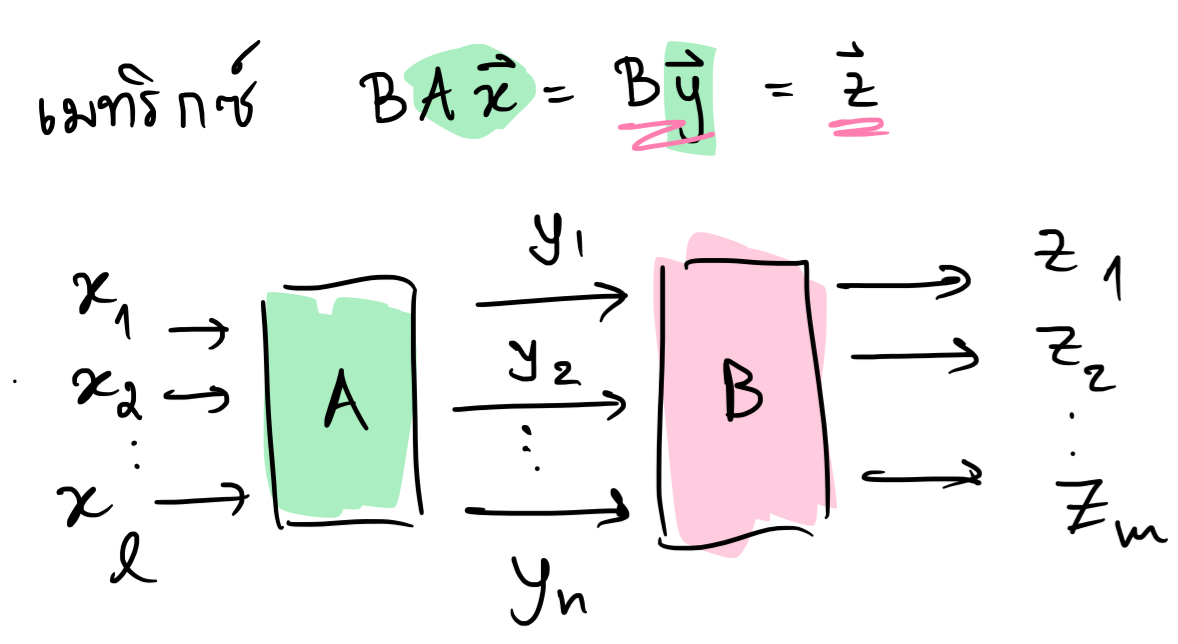จากภาพเราจะเห็นว่า output ของ $A$ คือ input ของ $B$ การคูณกันได้ของเมทริกซ์จึงขึ้นกับแค่จำนวนหลักหรือแถวของเมทริกซ์ ในขณะที่ขนาดของ input ของ $A$ และ output ของ $B$ สามารถเป็นอะไรก็ได้

สรุป

เราสามารถมองได้ว่าเมทริกซ์เป็นตัวแทนของฟังก์ชันเชิงเส้นหลายตัวแปรต้น หลายตัวแปรตาม (หลาย input หลาย output) การคูณเมทริกซ์กับเวกเตอร์เป็นการใส่ตัวแปรต้นลงไปในฟังก์ชันเชิงเส้น และการคูณเมทริกซ์กับเมทริกซ์เป็นการกระชับฟังก์ชันเชิงเส้นที่ประกอบต่อ ๆ กัน ให้กลายเป็นฟังก์ชันเชิงเส้นอันเดียว

ตอนนี้เป็นตอนสุดท้ายในชุดบทความนี้ คิดเห็นกันอย่างไรมาคอมเมนท์แนะนำติชมได้ในเพจ “บล็อกของทกล้า”