เรารู้ว่ามีสิ่งที่เรียกว่าจำนวนจินตภาพอยู่ นั่นคือจำนวนที่เป็นรากที่สอง (Square root) ของจำนวนที่เป็นลบ เช่น รากที่สองของลบหนึ่งแทนด้วย $i:=\sqrt{-1}$ พอได้ยินคำว่า “จินตภาพ” ทำให้หลายคนคิดไปว่าจำนวนจินตภาพมีอยู่แค่ในจินตนาการ ไม่ได้มีอยู่จริง ประกอบกับความคิดที่ว่าจำนวนที่มีอยู่จริงจะต้องวัดค่าของมันออกมาได้ แต่จำนวนจินตภาพไม่มีสถานการณ์ที่เห็นได้ง่ายในชีวิตประจำวันที่เราอะไรแล้วได้ค่าเป็นจำนวนจินตภาพ ก็ยิ่งพาให้เราคิดว่าจำนวนจินตภาพนี้ไม่ได้มีอยู่จริง เป็นเพียงจินตนาการของนักคณิตศาสตร์เท่านั้น

ในทางกลับกัน ในบทความนี้จะพาทุกคนกลับมาตั้งคำถามกับความเชื่อโดยไม่ได้ตั้งข้อสงสัย ว่าจำนวนจริงทุกจำนวนนั้นมีอยู่จริง จริง ๆ หรือ

มีอยู่จริงในที่นี้มีความหมายในทำนองเดียวกันกับการตั้งคำถามกับจำนวนจินตภาพ เราจะพาตั้งคำถามว่าเราวัดค่าบางอย่างให้ออกมาเป็นจำนวนจริงได้หรือไม่ แน่นอนว่าเราวัดและจับต้องจำนวนที่เป็นจำนวนเต็ม เศษส่วนได้อยู่แล้ว สิ่งที่น่าสงสัยที่สุดก็คือจำนวนที่ไม่ได้เป็นเศษส่วนอย่างจำนวนอตรรกยะ (irrational numbers) เช่น $\pi$, $\sqrt{2}$, $\sqrt{3}$, หรือ $\varphi$ (สัดส่วนทองคำ)

อะไรเป็นจำนวนจริงบ้าง

การให้คำนิยามของจำนวนจริง เช่น จำนวนจริงคือจำนวนที่อยู่บนเส้นจำนวนจริง จำนวนทุกจำนวน จำนวนที่มีอยู่จริง เหล่านี้ เป็นนิยามที่อาจจะพอทำให้เห็นภาพ แต่ก็ไม่ได้รัดกุมเท่าใดนักและสุ่มเสี่ยงที่จะสร้างความเข้าใจผิด

ในบทความนี้เราจะไม่ได้อธิบายว่าจำนวนจริงคืออะไร นิยามอย่างไร แต่จะบอกว่าในเซตของจำนวนจริง $\mathbb{R}$ ประกอบไปด้วยอะไรบ้าง

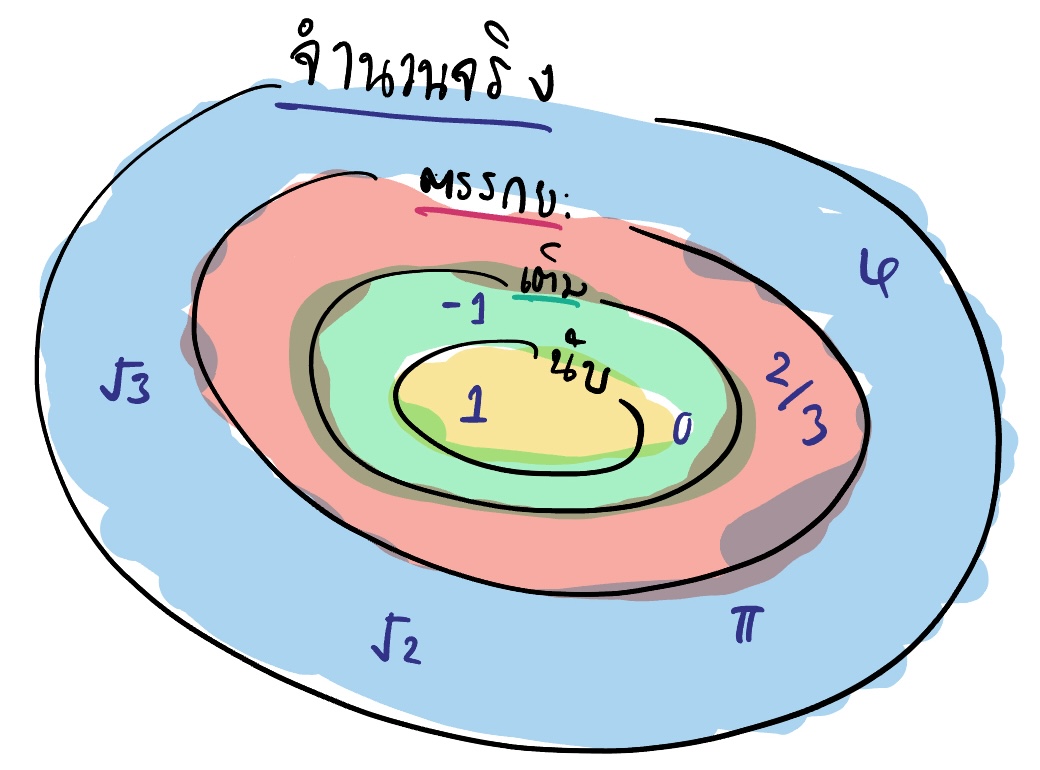
ในเซตของจำนวนจริงมี

• จำนวนนับ $\mathbb{N}$ (เช่น $1, 2, 3, \ldots$)
• จำนวนเต็ม $\mathbb{Z}$ (เช่น $\ldots, -2, -1, 0, 1, 2, \ldots$)
• จำนวนตรรกยะ $\mathbb{Q}$ (จำนวนที่เป็นเศษส่วนของจำนวนเต็ม เช่น $\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \ldots$)
• จำนวนอตรรกยะ $\mathbb{R}\setminus\mathbb{Q}$ (เครื่องหมาย $\setminus$ หมายถึง เซตของสมาชิกใน $\mathbb{R}$ ที่ไม่อยู่ในเซต $\mathbb{Q}$)

จำนวนอตกรรยะเป็นจำนวนที่สำคัญมากในการสร้างเซตของจำนวนจริงขึ้นมา หากไม่มีจำนวนอตรรกยะอยู่ในเซตนี้ เซตนี้จะเรียกว่าเป็นเพียงจำนวนตรรกยะเท่านั้น

จำนวนอตรรกยะคืออะไร

อย่างที่เกริ่นไปก่อนหน้า ว่าจำนวนที่น่าสงสัยที่สุดว่าเราวัดค่าออกมาได้จริง ๆ หรือไม่ คือจำนวนอตรรกยะ เช่น $\pi$, $\sqrt{2}$, $\sqrt{3}$,

เพื่อที่จะทำให้พอเห็นภาพ สมบัติของจำนวนอตกรรยะเป็นดังนี้

1. จำนวนอตรรกยะเป็นจำนวนที่ไม่สามารถเขียนเป็นเศษส่วนของจำนวนเต็มได้
2. จำนวนอตรรกยะเป็นทศนิยมไม่รู้จบ

โปรดระมัดระวังว่าบทกลับของสมบัติข้างต้นไม่จำเป็นจะเป็นจริง

1. จำนวนที่ไม่สามารถเขียนเป็นเศษส่วนของจำนวนเต็มได้ไม่จำเป็นต้องเป็นจำนวนอตรรกยะ เช่น $i$
2. จำนวนที่เป็นทศนิยมไม่รู้จบไม่จำเป็นต้องเป็นจำนวนอตรรกยะ เช่น $\frac{1}{3} = 0.33…$

การวัด และค่าคลาดเคลื่อน

เปลี่ยนโหมดมาเป็นนักฟิสิกส์บ้าง การวัดมีค่าคลาดเคลื่อน หรือค่าความไม่แม่นยำ (error) ที่เกิดขึ้นได้ เช่น เราใช้ไม้บรรทัดวัดขนาดของกระดาษ เราก็จะได้ทศนิยมมา 1 หรือ 2 ตำแหน่งในหน่วยเซนติเมตร สมมติเราวัดได้แม่นยำในทศนิยม 1 ตำแหน่งนั่นหมายความว่าเรามั่นใจในขีดย่อยของไม้บรรทัด (ขีด 1 มิลลิเมตร) และความคลาดเคลื่อนอยู่ในหน่วยทศนิยมถัดไป ถ้าเราทำให้ค่าคลาดเคลื่อนนี้เล็กลงไปอีก เช่นจากคลาดเคลื่อนในตำแหน่งที่สอง เราสร้างสุดยอดไม้บรรทัดที่วัดค่าคลาดเคลื่อนให้อยู่ในตำแหน่งที่ 3 ได้ แต่เราก็ยังไม่สามารถวัดค่าคลาดเคลื่อนให้อยู่ในตำแหน่งที่ 4 ได้ และค่าคลาดเคลื่อนจะอยู่ในหน่วยทศนิยมถัดไปเรื่อย ๆ

ตัวอย่างเช่น เราวัดกระดาษด้วยไม้บรรทัดได้ความยาว $2.7$ เซนติเมตร นั่นหมายความว่าเรามีทศนิยมหลักถัดไปที่เราไม่รู้แน่ชัดว่าเป็นเท่าใด ค่าความยาวจริง ๆ ที่เราวัดได้อาจจะอยู่ในช่วง $[2.65, 2.75)$ เซนติเมตร เช่นเดียวกันถ้าเราวัดได้ละเอียดขึ้น เช่น วัดได้ $2.71$ เซนติเมตร นั่นหมายความว่าค่าความยาวจริงอาจจะอยู่ในช่วง $[2.705, 2.715)$ เซนติเมตร

ดังนั้นเวลาที่เราวัดค่าปริมาณทางฟิสิกส์ออกมา เราไม่ได้วัดออกมาเป็นค่าค่าเดียวที่แม่นยำ แต่เราได้ออกมาเป็นช่วงของค่านั้น ช่วงจะกว้างหรือแคบเท่าใดก็ขึ้นกับว่าการวัดนั้นมีความแม่นยำเท่าใด

คำถามที่สำคัญกับเรื่องนี้คือ เราจะต้องวัดค่าให้แม่นยำเท่าไหร่เราจึงจะมั่นใจได้ว่าค่าจริง ๆ ของสิ่งที่เราวัดเป็นจำนวนอตรรกยะ

คำถามนี้เท่ากับคำถามที่ว่าช่วงของตัวเลขในจำนวนจริงที่มีแต่จำนวนอตรรกยะเป็นเท่าไหร่ คำตอบก็คือกว้างเท่ากับ 0 หรือเราต้องวัดให้แม่นเป๊ะเท่านั้นเราจึงจะมั่นใจได้ว่าค่าที่เราวัดได้เป็นจำนวนอตรรกยะ นั่นเป็นเพราะว่าในช่วงเล็ก ๆ รอบ ๆ จำนวนจริงใด ๆ (รวมถึงจำนวนอตรรกยะ) จะมีจำนวนตรรกยะอยู่ในช่วงนั้นเสมอ

ช่วงเล็ก ๆ รอบ ๆ จำนวนจริงใด ๆ

ความหมายแบบรัดกุม สมมติว่าเรามีจำนวนจริงใด ๆ $p$ และพิจารณาช่วงเล็ก ๆ รัศมี $\varepsilon$ รอบ ๆ $p$ คือ $(p-\varepsilon, p+\varepsilon)$ เราสามารถพิสูจน์ได้ว่า เรามีจำนวนตรรกยะอยู่ในช่วงนี้เสมอ

พิสูจน์ สมมติว่า $p$ เป็นจำนวนจริงใด ๆ และ $\varepsilon$ เป็นจำนวนจริงบวกใด ๆ เราจะได้ว่า $p-\varepsilon$ และ $p-\varepsilon$ เป็นจำนวนจริง เราเรียก $x$ และ $y$ แทนสองค่านี้ $$x:=p-\varepsilon$$ $$y:=p+\varepsilon$$ เรารู้ว่าจำนวนจริงทุกจำนวนสามารถเขียนเป็นทศนิยมได้ (รู้จบหรือไม่ก็ตาม) เราแทนทศนิยมของ $x$ และ $y$ ด้วย $$x:=x_0.x_1x_2x_3\ldots$$ $$y:=y_0.y_1y_2y_3\ldots$$ เรารู้ว่า y > x เพราะว่า $\varepsilon$ เป็นจำนวนจริงบวก จะต้องมีจำนวนเต็ม $n$ ที่ทำให้ $y_n > x_n$

ทำให้เราสร้างจำนวนตรรกยะ เรียกแทนว่า $q$ ได้ดังนี้ $$ q:=x_0.x_1x_2x_3\ldots x_n 1$$ เป็นทศนิยมรู้จบ ดังนั้นเป็นจำนวนตรรกยะ และอยู่ในช่วง $(p-\varepsilon, p+\varepsilon)$

ตัวอย่าง

เรารู้ว่าจำนวนอตรรกยะบางตัว สร้างได้จากรูปเลขาคณิต เช่นสามเหลี่ยมมุมฉากที่มีด้านทั้งสองด้านยาวเท่ากับ 1 หน่วย จะมีด้านตรงข้ามมุมฉากเท่ากับ $\sqrt{2}$ หน่วย

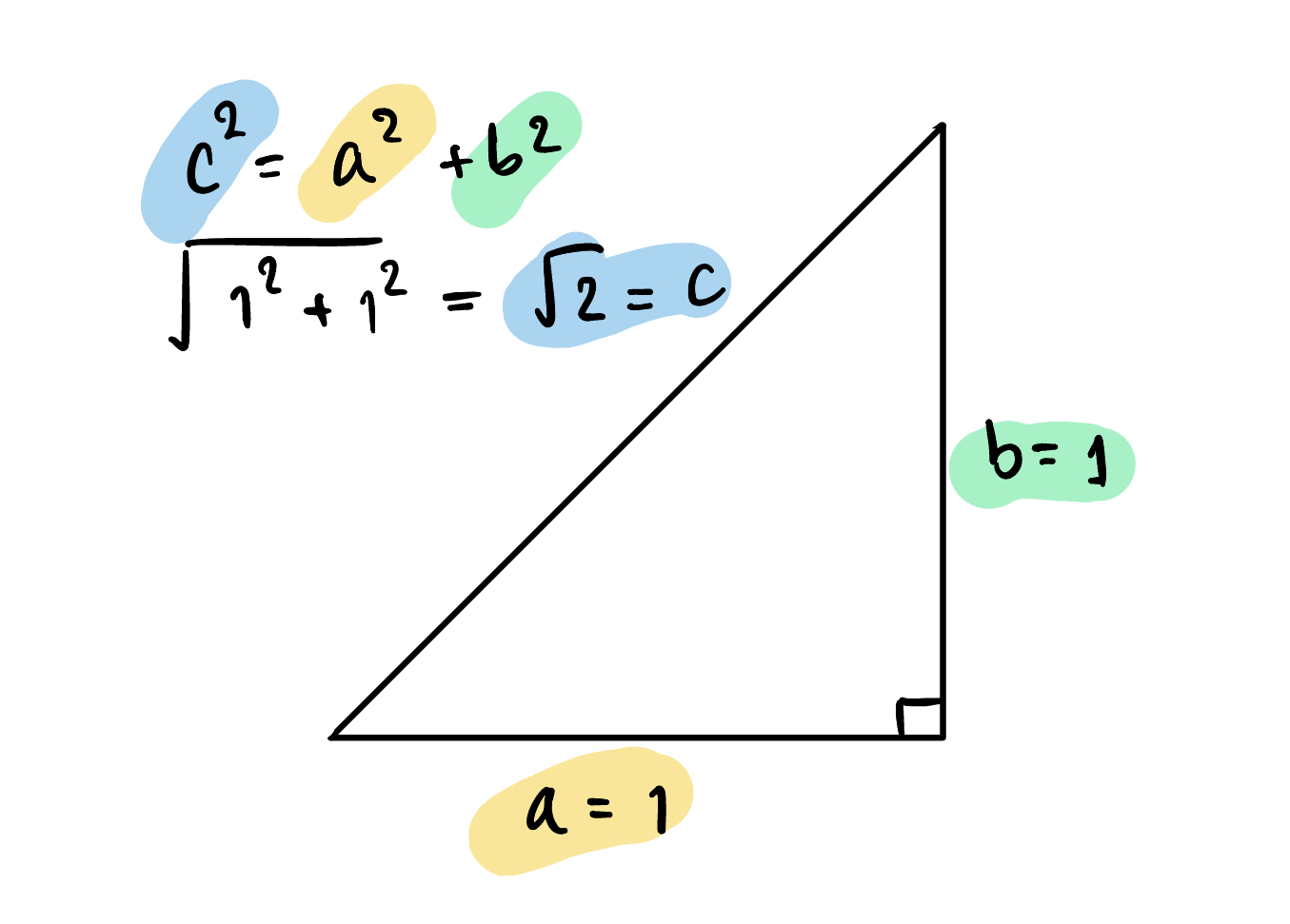
แต่เวลาเราสร้างรู้สามเหลี่ยมขึ้นมาเพื่อที่จะได้ความยาวของด้านทั้งสองด้านเท่ากับหนึ่งหน่วยพอดี เราต้องใช้เครื่องมือที่แม่นยำแบบเป๊ะๆ ไม่อย่างนั้นเราก็จะได้ด้านตรงข้ามมุมฉากที่มีความคลาดเคลื่อน สมมติว่าค่าความคลาดเคลื่อนนี้เป็น $\pm\sqrt{2}/100$ นั่นคือช่วงของความยาวด้านตรงข้ามมุมฉากที่เราสร้างขึ้นมา จริง ๆ แล้วคือสักค่าในช่วง $(\sqrt{2}-\sqrt{2}/100,\sqrt{2}+\sqrt{2}/100)$ นั่่นคือ x และ y ในที่นี่คือ $$x=\sqrt{2}-\sqrt{2}/100 = 1.4007…$$ $$y=\sqrt{2}+\sqrt{2}/100 = 1.4283…$$

ในช่วงนี้มีจำนวนที่เป็นจำนวนตรรกยะอยู่ หนึ่งในนั้นก็คือ $$q=1.401$$ ซึ่งจำนวนที่สร้างอย่างในบทพิสูจน์ก่อนหน้า

สรุป

ทั้งบทพิสูจน์และตัวอย่างนี้เป็นการพิสูจน์ว่า ในช่วงเล็ก ๆ รอบ ๆ จำนวนจริงใด ๆ จะมีจำนวนตรรกยะอยู่เสมอ ดังนั้นหากเราอยากรู้แน่ ๆ ว่าจะวัดค่าที่เป็นจำนวนอตรรกยะออกมาได้จริง ๆ ไหม เราต้องวัดค่าให้ได้อย่างแม่นเป๊ะ

หากเราคิดว่าจำนวนจะมีอยู่จริงก็ต่อเมื่อเราวัดค่ามันออกมาได้จริง ๆ จำนวนอตรรกยะอาจจะไม่มีอยู่จริง เพราะเราต้องวัดได้ให้แม่นยำสมบูรณ์ เมื่อส่วนประกอบสำคัญของจำนวนจริงไม่มีอยู่จริง เซตของจำนวนจริงที่เราเผลอคิดว่ามีจริง ก็อาจจะไม่มีอยู่จริงด้วย

อ่านเพิ่ม

การมีอยู่จริงของจำนวน (จำนวนจริง หรือ จำนวนเซิงซ้อนก็ตาม) เป็นความจริงแบบคณิตศาสตร์ซึ่งแตกต่างกับความจริงที่เราพูดถึงในความจริงแบบวิทยาศาสตร์ (ธรรมชาติ) ผมเคยเขียนเรื่องนี้ไว้บน Medium สามารถอ่านได้ที่นี่