นอกจากการแก้สมการที่ได้พูดถึงไปในตอนที่ 1 แล้ว การคูณเมทริกซ์ยังมีความหมายอื่นอีก ในตอนนี้เราจะมาดูตัวอย่างว่าการคูณเมทริกซ์ในบริบทนอกจากการแก้สมการแล้ว ให้ความหมายอะไร สามารถใช้ไปซื้อผักได้หรือไม่

หนูนิดไปซื้อผักที่ตลาด

ขอสมมติตัวละครหลักให้ชื่อว่าหนูนิด หนูนิดเป็นคนที่ออกจากบ้านไปซื้อผักที่ตลาดให้กับครอบครัวตอน 7 โมงเช้าทุกวัน แต่ก่อนจะไปซื้อผัก หนูนิดจะต้องแวะไปซื้อหนังสือพิมพ์ท้องถิ่นจากร้านหนังสือให้กับป้าข้างบ้าน และหลังจากนั้นค่อยไปซื้อผักที่ตลาด และค่อยกลับมาบ้าน สมมติว่าบ้าน ตลาด และร้านหนังสืออยู่ห่างกัน 5 นาที

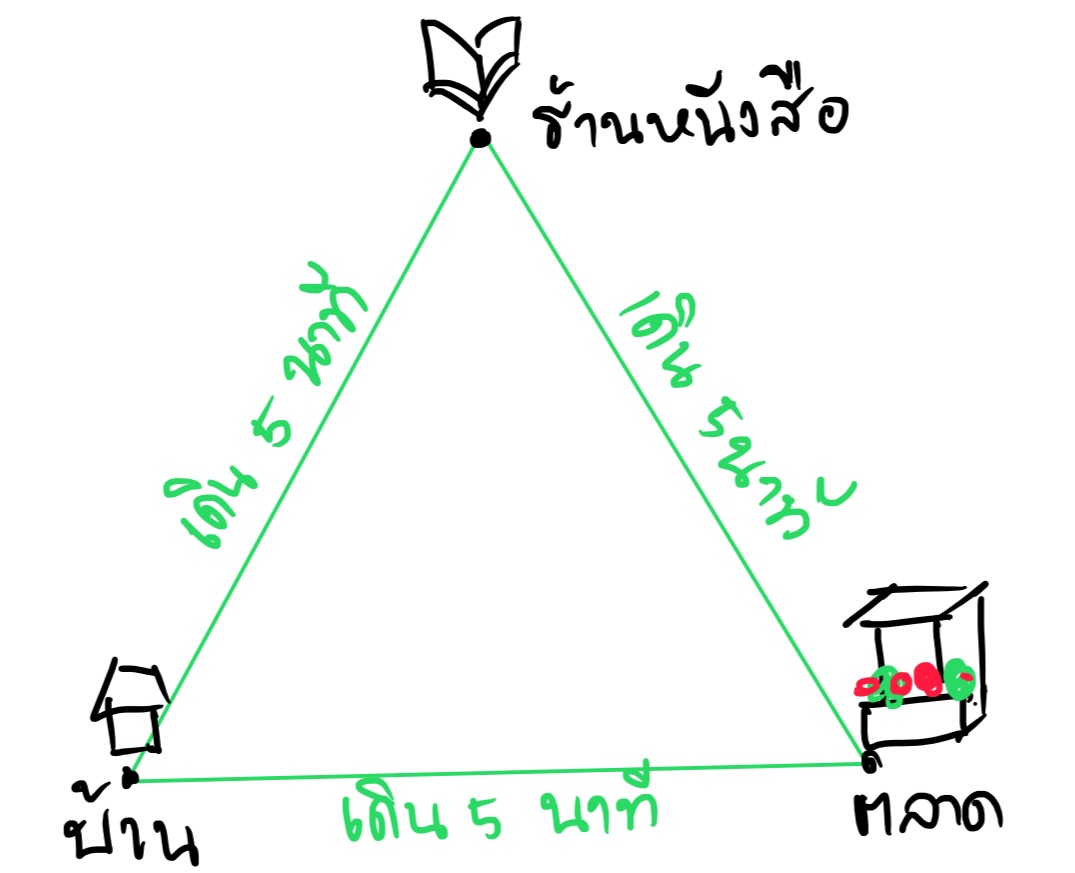
ถ้าเราดูว่าทุก ๆ 5 นาทีหนูนิดอยู่ที่ใด บ้าน ตลาด หรือร้านหนังสือ เราสามารถใช้เมทริกซ์มาบรรยายการเปลี่ยนตำแหน่งของหนูนิดได้ดังต่อไปนี้

เมทริกซ์และการเดินทางของหนูนิด

เริ่มแรก เราจะแทนตำแหน่งของหนูนิดด้วย เลขหนึ่ง ในคอลัมน์เวกเตอร์​ $\vec{n}$ (คอลัมน์เวกเตอร์คืออเมทริกซ์ที่มีเพียง 1 คอลัมน์) และเริ่มต้นด้วยตำแหน่งของหนูนิดที่บ้าน ดังนี้ $$\vec{n} = \begin{pmatrix}1\\0\\0\end{pmatrix}$$ ถ้าหนูนิดอยู่ที่ร้านหนังสือ เลขหนึ่งก็จะมาอยู่ที่แถวที่สองของเวกเตอร์ $\vec{n}$ และถ้าหนูนิดอยู่ที่ตลาด เลขหนึ่งก็จะมาอยู่ที่แถวที่สามของเวกเตอร์ $\vec{n}$

เรารู้ว่าตอน 7 โมงเช้า ในอีก 5 นาทีหนูนิดจะอยู่ที่ร้านหนังสือเพื่อซื้อหนังสือพิมพ์ให้ป้าข้างบ้าน ใน 5 นาทีถัดไปก็จะอยู่ที่ตลาดเพื่อซื้อผักและอีกห้านาทีถัดไปก็จะกลับมาที่บ้าน การเปลี่ยนตำแหน่งทั้งหมดของหนูนิดนี้สามารถบรรยายได้ด้วยเมทริกซ์ $T$ $$ T := \begin{pmatrix}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{pmatrix}$$

การเดินทางของหนูนิด = การคูณเมทริกซ์กับเวกเตอร์ตำแหน่ง

ถ้ายังไม่เชื่อว่าบรรยายได้ ก็ลองคูณเมทริกซ์นี้กับตำแหน่งเริ่มต้นของหนูนิดดู

หลังจากออกจากบ้านไปได้ 5 นาที หนูนิดจะอยู่ที่ร้านหนังสือ ดังนั้นตำแหน่งของหนูนิดจะเปลี่ยนไปเป็น $$T \vec{n} = \begin{pmatrix}0 & 0 & 1\\ \textcolor{blue}{1} & 0 & 0\\ 0 & 1 & 0\end{pmatrix}\begin{pmatrix}\textcolor{blue}{1}\\0\\0\end{pmatrix} = \begin{pmatrix}0\\ \textcolor{blue}{1}\\0\end{pmatrix}$$ อันนี้คือหนูนิดอยู่ที่ร้านหนังสือพิมพ์ ขอทบทวนว่า เวลาที่เราคูณเมทริกซ์กับเวกเตอร์ เราเอาแถวแต่ละแถวไปคูณกับคอลัมน์ของเวกเตอร์ เช่นเอาแถวที่ 1 ไปคูณกับเวกเตอร์และใส่ผลลัพธ์ไว้ที่แถวที่ 1 ของเวกเตอร์ผลลัพธ์ สำหรับกรณีนี้การคูณกับทุกตัวยกเว้นตัวสีน้ำเงินจะได้ผลลัพธ์เป็นศูนย์

หลังจากออกจากบ้านไปได้ 10 นาที หนูนิดจะอยู่ที่ร้านหนังสือ ดังนั้นตำแหน่งของหนูนิดจะเปลี่ยนไปเป็น $$T(T \vec{n}) = \begin{pmatrix}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & \textcolor{blue}{1} & 0\end{pmatrix}\begin{pmatrix}0\\ \textcolor{blue}{1}\\0\end{pmatrix} = \begin{pmatrix}0\\0\\ \textcolor{blue}{1}\end{pmatrix}$$ ส่วนอันนี้แปลว่าหนูนิดอยู่ที่ตลาดและกำลังซื้อผักอยู่

พอออกจากบ้านได้ครบ 15 นาที หนูนิดก็กลับมาที่บ้าน $$T (T(T \vec{n})) = \begin{pmatrix}0 & 0 & \textcolor{blue}{1}\\ 1 & 0 & 0\\ 0 & 1 & 0\end{pmatrix}\begin{pmatrix}0\\0\\ \textcolor{blue}{1}\end{pmatrix} = \begin{pmatrix}\textcolor{blue}{1}\\0\\0\end{pmatrix}$$

ลองสังเกตว่าสำหรับการออกไปได้ 5 นาที เมทริกซ์ $T$ คูณเวกเตอร์​ $\vec{n}$ ไปครั้งเดียว แต่สำหรับการออกไปได้ 10 นาที เมทริกซ์ $T$ คูณเวกเตอร์​ $\vec{n}$ ไปสองครั้ง และสำหรับการออกไปได้ 15 นาที เมทริกซ์ $T$ คูณเวกเตอร์​ $\vec{n}$ ไปสามครั้ง แทนที่เราจะคูณเวกเตอร์ด้วยเมทริกซ์หลาย ๆ ครั้ง เราสามารถคูณเมทริกซ์ด้วยเมทริกซ์ได้เลย และเมทริกซ์ที่ได้ก็จะบรรยายการเปลี่ยนตำแหน่งของหนูนิดได้เช่นเดียวกัน $$ T(T \vec{n}) = (TT)\vec{n} = T^2 \vec{n} $$ อันนี้เป็นสมบัติของการคูณเมทริกซ์ที่เรียกว่า สมบัติการจัดกลุ่ม (associative property) ของการคูณเมทริกซ์

หนูนิดไปไหนมา = หาเมทริกซ์ผกผัน

สมมติว่าเรารู้พฤติกรรมการเดินของหนูนิด (เทียบเท่ากับรู้หน้าตาของเมทริกซ์ $T$) เราสามารถบอกได้เลยว่าหนูนิดไปไหนมา เพียงแค่รู้ว่าตอนนี้หนูนิดอยู่ที่ไหน เพราะว่าเราสามารถหา “เมทริกซ์ผกผัน” (inverse matrix) $T^{-1}$ ของหนูนิดได้ เพราะว่าดีเทอร์มิเนนท์ของเมทริกซ์ $T$ เท่ากับ 1 เมทริกซ์ผกผันจึงเหมือนกับการบรรยายการเดินทางของหนูนิดแต่ย้อนเวลากลับ

ทีดียิ่งกว่าก็คือเมทริกซ์ผกผันของการเดินทางของหนูนิด ก็คือเมทริกซ์สลับเปลี่ยน (transpose matrix) ของ $T$ เขียนแทนด้วย $T^T$ (เมทริกซ์สลับเปลี่ยนจะเปลี่ยนแถวของเมทริกซ์ต้นฉบับให้เป็นคอลัมน์และจากคอลัมน์เป็นแถว) $$ T^{-1} = \begin{pmatrix}0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\end{pmatrix} = T^T$$ คำเตือน สมบัตินี้ไม่ได้เป็นสมบัติที่มีสำหรับทุก ๆ เมทริกซ์จตุรัส เมทริกซ์ที่มีสมบัตินี้เรียกว่า orthogonal matrix

ถ้าไม่เชื่อว่าเมทริกซ์ผกผันของ $T$ คือ $T^T$ ก็ลองคูณเมทริกซ์ $T$ กับ $T^T$ ดู เราจะได้เมทริกซ์เอกลักษณ์ (identity matrix) ออกมา ซึ่งการคูณเมทริกซ์เอกลักษณ์กับเวกเตอร์จะได้เวกเตอร์เดิมออกมาเสมอ การคูณ $T^TT$ กับเวกเตอร์ตำแหน่ง $n$ ก็เหมือนกับให้หนูนิดเดินไปและก็เดินกลับมาที่เดิม

หนูนิดเดินสุ่ม

สมมติว่าหนูนิดอยากจะเล่นเกมกับตัวเอง ตอน 7 โมงเช้า แทนที่จะเดินออกจากบ้านไปที่ร้านหนังสือพิมพ์อย่างที่เคยทำ หนูนิดจะทอยเหรียญ ถ้าออกหัวหนูนิดก็จะไปร้านหนังสือพิมพ์ แต่ถ้าออกก้อยหนูนิดก็จะไปซื้อผักก่อน แล้วค่อยไปร้านหนังสือพิมพ์ พออยู่ที่ร้านหนังสือ (หรือที่ตลาด) หนูนิดก็ทอยเหรียญอีกว่าจะเดินไปที่บ้าน หรือเดินไปที่ตลาด (หรือที่ร้านหนังสือ)

ทีนี้เราจะไม่สามารถบรรยายได้ด้วยเมทริกซ์เดิมแล้ว แต่ก็ยังบรรยายการเดินทางไปซื้อผักของหนูนิดได้ด้วยเมทริกซ์ใหม่ ขอเรียกว่าเป็นเมทริกซ์ $S$

การคูณเมทริกซ์และโอกาสที่จะเจอหนูนิด

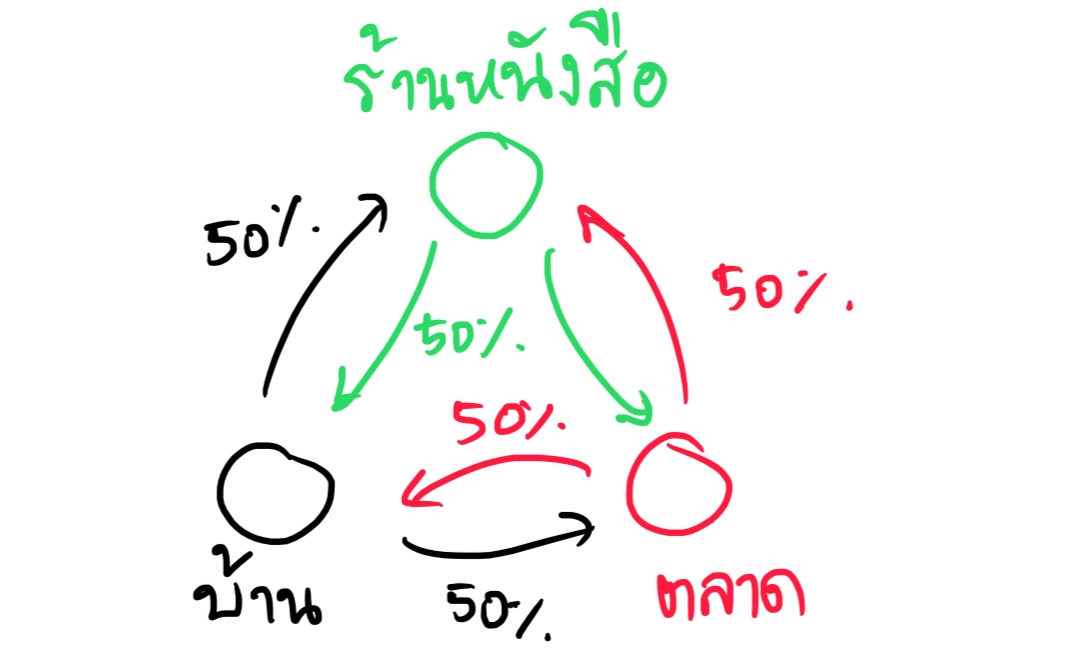
เราสามารถแปลงสิ่งที่เมทริกซ์ $S$ ควรจะทำกับเวกเตอร์ตำแหน่งของหนูนิดได้ดังนี้

ถ้าหนูนิดอยู่ที่บ้านจะมีโอกาส 50% ที่จะเดินไปที่ร้านหนังสือพิมพ์ และ 50% ที่จะไปซื้อผักที่ตลาด นั่นหมายความว่า เมทริกซ์ $S$ ทำกับเวกเตอร์ของตำแหน่งของหนูนิด จะได้เวกเตอร์ที่บอกว่าหนูนิดจะมีโอกาสไปที่ร้านหนังสือพิมพ์กับตลาดเท่าๆ กัน คือ $$S\begin{pmatrix}1 \\0\\0\end{pmatrix} = \begin{pmatrix}0 \\ \frac{1}{2}\\ \frac{1}{2}\end{pmatrix} $$

ถ้าหนูนิดอยู่ที่ร้านหนังสือพิมพ์ หนูนิดจะมีโอกาส 50% ที่จะกลับมาที่บ้าน และ 50% ที่จะไปซื้อผักต่อ $$S\begin{pmatrix}0 \\1\\0\end{pmatrix} = \begin{pmatrix}\frac{1}{2} \\ 0\\ \frac{1}{2}\end{pmatrix} $$

เช่นเดียวกัน ถ้าหนูนิดอยู่ที่ตลาด หนูนิดจะมีโอกาส 50% ที่จะไปที่ร้านหนังสือพิมพ์ และ 50% ที่จะกลับมาที่บ้าน $$S\begin{pmatrix}0 \\0\\1\end{pmatrix} = \begin{pmatrix}\frac{1}{2} \\ \frac{1}{2}\\ 0\end{pmatrix} $$

พอเรารู้ว่าเมทริกซ์ทำกับเวกเตอร์สามตัวนี้อย่างไร เราก็สามารถที่จะสร้างเมทริกซ์ $S$ ขึ้นมาได้ ดังนี้ $$ S = \begin{pmatrix} 0 & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{2}& \frac{1}{2} & 0 \end{pmatrix}$$

สังเกตว่าคอลัมน์ที่หนึ่งคือผลคูณระหว่างเมทริกซ์ $S$ กับเวกเตอร์ $\vec{n} = (1 , 0 , 0)^T$ ที่แสดงตำแหน่งของหนูนิดที่บ้าน คอลัมน์ที่สองคือผลคูณระหว่างเมทริกซ์ $S$ กับเวกเตอร์ $\vec{n} = (0 , 1 , 0)^T$ ที่แสดงตำแหน่งของหนูนิดที่ร้านหนังสือพิมพ์ และคอลัมน์ที่สามคือผลคูณระหว่างเมทริกซ์ $S$ กับเวกเตอร์ $\vec{n} = (0 , 0 , 1)^T$ ที่แสดงตำแหน่งของหนูนิดที่ตลาด

หนูนิดอยู่ที่ไหน?

ยิ่งไปกว่านั้น ถ้าเราไม่ได้มีข้อมูลแน่ชัดว่าหนูนิดอยู่ที่ใด เช่นเรารู้ว่าหนูนิดเริ่มเดินที่บ้าน ผ่านไปแล้วห้านาที เราไม่ได้ไปถามหนูนิดว่าหนูนิดอยู่ที่ใดระหว่างที่ตลาดกับร้านหนังสือ แต่เรารู้ว่ามีโอกาส 50:50 ที่หนูนิดจะอยู่ที่ตลาดและร้านหนังสือ

เราสามารถทำนายได้ว่าโอกาสที่จะเจอหนูนิดในที่ต่าง ๆ ในอีก 5 นาทีถัดไปจะเป็นเท่าไหร่ โดยการคูณเมทริกซ์ $S$ กับเวกเตอร์ตำแหน่งของหนูนิด ดังนี้ $$S\vec{n} = \begin{pmatrix} 0 & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{2}& \frac{1}{2} & 0 \end{pmatrix}\begin{pmatrix}0\\ \frac{1}{2}\\ \frac{1}{2}\end{pmatrix} = \begin{pmatrix}\frac{1}{2} \\ \frac{1}{4}\\ \frac{1}{4}\end{pmatrix}$$ นั่นคือมีโอกาส 50% ที่ในอีกห้านาทีถัดไป หนูนิดจะอยู่ที่บ้าน และมีโอกาส 25% ที่หนูนิดจะอยู่ที่ร้านหนังสือพิมพ์ และมีโอกาสอีก 25% ที่หนูนิดจะอยู่ที่ตลาด

ค่าโอกาสนี้มีค่าเท่ากันกับการที่เรามาแจกแจงกรณีที่หนูนิดอยู่ที่ตลาดและร้านหนังสือพิมพ์ และค่อย ๆ คำนวณหาโอกาสของสถานที่ถัดไปที่หนูนิดจะไป ดังนี้

หนูนิดมีโอกาส 50% ที่จะเริ่มที่ตลาด และ 50% ที่จะเริ่มที่ร้านหนังสือพิมพ์

ถ้าเริ่มต้นหนูนิดอยู่ที่ตลาด หนูนิดจะมีโอกาส 50% ที่จะไปที่ร้านหนังสือพิมพ์ และ 50% ที่จะกลับมาที่บ้าน

ถ้าเริ่มต้นหนูนิดอยู่ที่ร้านหนังสือพิมพ์ หนูนิดจะมีโอกาส 50% ที่จะกลับมาที่บ้าน และ 50% ที่จะไปที่ตลาด

เราจะได้ว่า
หนูนิดมีโอกาส $\frac{50}{100}\times\frac{50}{100} =25 \% $ ที่จะเดินจาก ตลาด ไปที่ บ้าน
หนูนิดมีโอกาส $\frac{50}{100}\times\frac{50}{100} =25 \% $ ที่จะเดินจาก ตลาด ไปที่ ร้านหนังสือพิมพ์
หนูนิดมีโอกาส $\frac{50}{100}\times\frac{50}{100} =25 \% $ ที่จะเดินจาก ร้านหนังสือพิมพ์ ไปที่ ตลาด
หนูนิดมีโอกาส $\frac{50}{100}\times\frac{50}{100} =25 \% $ ที่จะเดินจาก ร้านหนังสือพิมพ์ ไปที่ บ้าน\

เราสนใจแค่่ว่าหนูนิดจะอยู่ที่ไหนในห้านาทีถัดไป สรุปได้คือ
หนูนิดมีโอกาส $25\% + 25\% = 50\% $ ที่จะจบที่ บ้าน
หนูนิดมีโอกาส $25\%$ ที่จะจบที่ ตลาด
และหนูนิดมีโอกาส $25\%$ ที่จะจบที่ ร้านหนังสือพิมพ์
ตรงกับที่การคูณเมทริกซ์บอกเราไว้

ผลรวมของเมทริกซ์ ถ่วงน้ำหนักด้วยความน่าจะเป็น

ทั้งหมดนี้เกิดขึ้นเพราะเราไม่รู้ว่าหนูนิดทายได้หัวหรือก้อย และหนูนิดไปที่ไหนมาแล้วบ้าง ถ้าเรารู้แน่ชัด เราก็สามารถที่จะเขียนเมทริกซ์ได้เลยว่าหนูนิดจะเดินทางอย่างไร เช่นว่าถ้าออกหัว เมทริกซ์ที่บรรยาการเดินทางก็จะเหมือนเดิม คือเมทริกซ์ $T$ ถ้าออกก้อย เมทริกซ์ที่บรรยายการเดินทางก็จะเปลี่ยนไป ขอเรียกว่าเป็นเมทริกซ์ $R$ $$R=\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1& 0 &0 \end{pmatrix}$$

ความน่าสนใจคือเมทริกซ์ $S$ เป็นผลรวมบางอย่างระหว่าง $T$ และ $R$ เรารู้ว่าถ้าหนูนิดทอยเหรียญจะมีโอกาส 50% ที่หนูนิดจะเดินตามเมทริกซ์ $T$ และมีโอกาสอีก 50% ที่หนูนิดจะเดินตามเมทริกซ์ $R$ ดังนั้นเมทริกซ์ $S$ ก็คือผลรวมของเมทริกซ์ $T$ และ $R$ ที่มีความน่าจะเป็นเท่า ๆ กัน $$S = \frac{1}{2}T + \frac{1}{2}R$$ ซึ่งเท่ากับเมทริกซ์ $S$ ที่เขียนไว้ก่อนหน้า $$S= \frac{1}{2}\begin{pmatrix}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{pmatrix} + \frac{1}{2}\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1& 0 &0 \end{pmatrix}=\begin{pmatrix} 0 & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{2}& \frac{1}{2} & 0 \end{pmatrix} $$ การที่เราเอาเมทริกซ์มารวมกันโดยที่สัมประสิทธิ์ (coefficient: ตัวเลขที่คูณกับเมทริกซ์) เป็นบวกและสัมประสิทธิ์ทุกตัวรวมกันได้ 1 เรียกว่า Convex combination

หนูนิดไปไหนมา อ่าว! ไม่มีเมทริกซ์ผกผันแล้ว

ในกรณีนี้ถ้าเรารู้เพียงว่าหนูนิดอยู่ที่ไหน เราไม่สามารถที่จะหาได้ว่าหนูนิดไปที่ไหนมา สิ่งนี้แสดงออกผ่านเมทริกซ์ $S$ ที่ไม่มีอินเวอร์ส (ไม่มีเมทริกซ์ผกผัน) จะรู้ได้ว่าเมทริกซ์ไหนมีอินเวอร์สหรือไม่ก็สามารถดูได้จากค่าดีเทอร์มิเนนต์ของเมทริกซ์ ซึ่งในกรณีนี้มีค่าเท่ากับศูนย์

สรุป

ทั้งหมดนี้เป็นการแสดงให้เห็นว่าการการเปลี่ยนตำแหน่งของหนูนิดบนแผนที่ระหว่างบ้าน ตลาดขายผัก และร้านหนังสือพิมพ์ สามารถแทนได้ด้วยการคูณระหว่างเมทริกซ์ที่บรรยายการเปลี่ยนที่ของหนูนิดกับ
เวกเตอร์ที่บรรยายตำแหน่งแห่งที่ของหนูนิด ยิ่งไปกว่านั้น แม้ว่าการเคลื่อนที่ของหนูนิดจะเป็นแบบสุ่ม ที่จะทอยเหรียญเพื่อตัดสินใจว่าจะไปที่ไหนดี เราก็ยังสามารถบรรยายการเปลี่ยนที่ของหนูนิดได้ด้วยเมทริกซ์ เวกเตอร์ของหนูนิด ก็บรรยายโอกาสที่จะเจอหนูนิดที่ตำแหน่งต่าง ๆ

ในบริบทนี้ ค่าดีเทอร์มิเนนต์บอกว่าเราสามารถที่จะหาได้หรือไม่ว่าหนูนิดไปที่ไหนมา เมทริกซ์อินเวอร์ส จึงเป็นเมทริกซ์ที่ให้หนูนิดย้อนกลับไปอยู่ที่ที่เคยมา ขยายความหมายและการประยุกต์ใช้มากไปกว่าการแก้สมการอย่างตอนที่แล้ว

สำหรับใครจะอยากจะอ่านเพิ่มเติม การเปลี่ยนตำแหน่งของหนูนิดในตัวอย่างนี้เป็นตัวอย่างหนึ่งของสิ่งที่เรียกว่า Markov chain มีประโยชน์ในหลายด้าน หนึ่งในนั้นคือการทำนายการระบาดของโรค และเมทริกซ์ที่บรรยายการเปลี่ยนที่ของหนูนิดเป็นเมทริกซ์ที่เรียกว่า stochastic matrix ให้เจาะจงเมทริกซ์ที่ใช้กับการเดินนี้เป็นเมทริกซ์ที่เรียกว่า doubly-stochastic matrix

หมายเหตุ

สำหรับตอนถัดไป จะพูดถึงโครงสร้างและนิยามทางคณิตศาสตร์ที่ทำให้การคูณเมทริกซ์เป็นอย่างที่มันเป็น