A wavefunction is a mathematical object which represents a quantum state. Many would have been introduced to wavefunctions from Schrödinger’s cat or the double-slit experiment. However, there is a more straightforward way to present the concept of wavefunction without resorting to the complex historical development of physics.
Often, the wavefunction is introduced by not knowing exactly where a particle is or its state. This is inaccurate because wavefunction is about something other than the lack of knowledge but the nature of quantum state and measurement.
In this article, I will introduce wavefunctions and superposition through the concept of matrices. I want to keep the concept of wavefunctions and the quantum state separate. While it is true that we can represent a specific kind of quantum state with wavefunctions, moving one step back from the physical context is an excellent way to develop a general understanding of the concept. Another preference of mine is to introduce this in the case of finite dimensions.
What is a wavefunction?
Mathematically speaking, a wavefunction is a vector of complex numbers whose ``2-norm’’ is 1. The 2-norm of a vector is a generalization of the length of the vector. For example, these are wavefunctions,
$$\begin{bmatrix}1\\0\end{bmatrix}, \frac{1}{\sqrt{2}} \begin{bmatrix}1\\ -1\end{bmatrix}, \frac{1}{\sqrt{3}} \begin{bmatrix}-1\\ i \\ 1 \end{bmatrix}.$$
The 2-norm of an $n$-dimensional vector is defined as
$$ \vert\vert v\vert\vert_2 := \left(\sum_{i=1}^n |v_i|^2\right)^{1/2}.$$
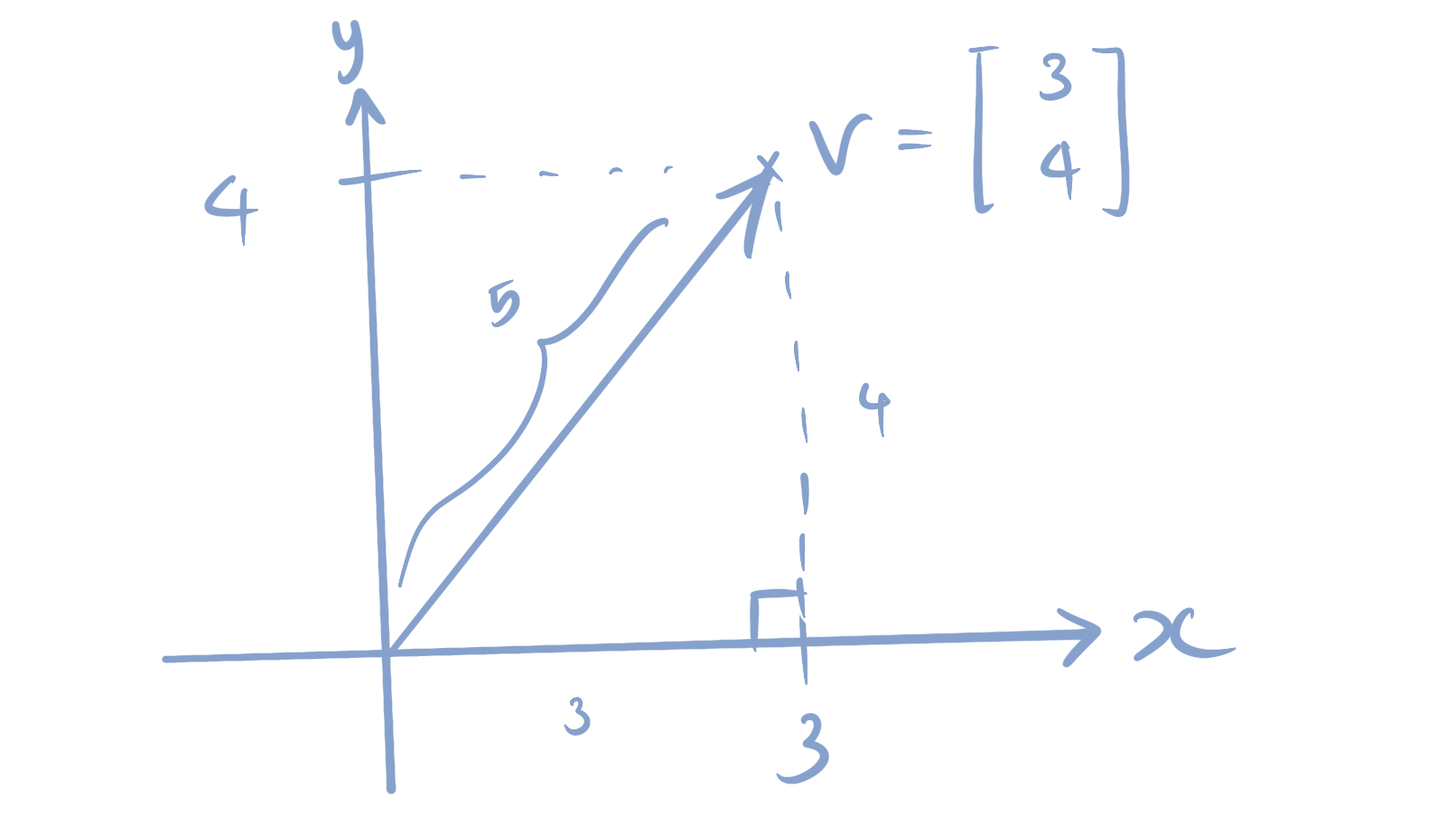
To intuitively understand this, we can think of 2-norm of a vector of 2 real numbers,
$$ v= \begin{bmatrix}3\\4\end{bmatrix}.$$
This vector is a vector of length $\sqrt{3^2+4^2} = \sqrt{25} = 5$.
What does a wavefunction say?
Consider a coin. We can represent the state of the coin by a vector of dimension 2. If the coin is head, it can be described with $\vert 0 \rangle = \begin{bmatrix}1\\0\end{bmatrix}$. The symbol $\vert 0 \rangle$ is called a ket; the notation system is named “bra-ket notation”. Analogue to this we have $\vert 1 \rangle = \begin{bmatrix}0\\1\end{bmatrix}$ representing the state of the coin being tail.
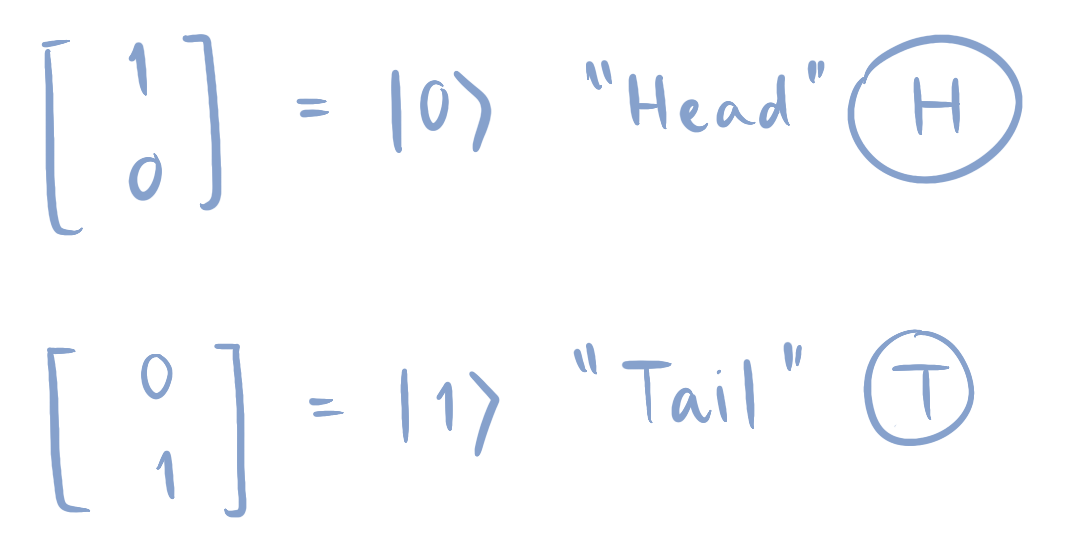
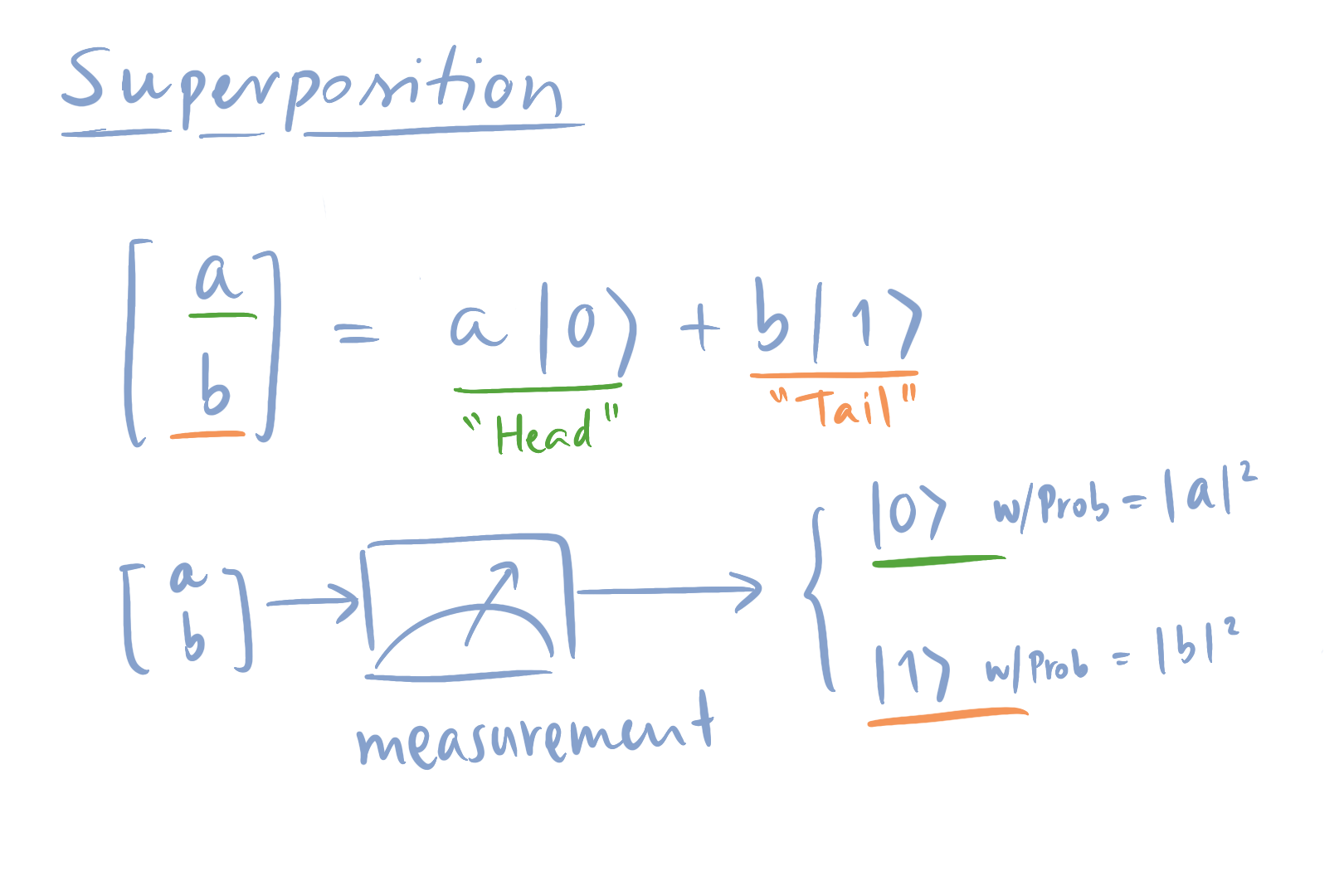
Wavefunctions allow us to have a state of coin in the superposition of head and tail. For example, $\frac{1}{\sqrt{2}} \begin{bmatrix}1\\1\end{bmatrix}$ is a state of coin that is in the superposition. Once we measure the coin concerning the basis of being head or tail, we get the result of head with probability $\frac{1}{2}$ and tail with probability $\frac{1}{2}$.
If we have a state $\vert \psi \rangle = \begin{bmatrix}a\\b\end{bmatrix}$, the probability of measuring the state to be $\vert 0 \rangle$ is $|a|^2$ and the likelihood of measuring the state to be $\vert 1 \rangle$ is $|b|^2$. Notice that as we interpret each vector element’s modulus square to be probability 1. This is also why we require the 2-norm of the wavefunction to be 1.
More generally, if we have $n$ possible states, we can represent the system’s state with a vector of dimension $n$. The probability of measuring the state to be in the state represented by $\vert i \rangle$ is $|v_i|^2$ where $v_i$ is the $i$-th element of the vector.
Transformation on wavefunctions
One of the best thing about quantum theories is that any transformation on wavefunction is linear. In the finite-dimensional case, we can represent any transformation with a matrix. One of the simplest transformations is the swapping between state $\vert 0 \rangle$ and $\vert 1 \rangle$. This transformation is represented by the matrix $$\mathrm{SWAP}\left(\vert 0 \rangle\right)= \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}0 \\ 1\end{bmatrix} = \vert 1 \rangle$$ A famous transformation is the Hadamard transformation. This transformation is represented by the matrix H $$H\vert 0 \rangle= \frac{1}{\sqrt{2}}\begin{bmatrix}1 & 1 \\ 1 & -1\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = \frac{1}{\sqrt{2}}\begin{bmatrix}1 \\ 1\end{bmatrix} = \frac{1}{\sqrt{2}}\left(\vert 0 \rangle + \vert 1 \rangle\right)$$ This will help us illustrate the distinction between wavefunctions and not knowing the state of the system.
Wavefunctions do not represent the lack of knowledge!
It’s a misconception to think about wavefunction as a cat in the box that we don’t know whether it is dead or alive. What I mean by the lack of knowledge is our ignorance of the actual state of the system.
To put it in our coin example, we don’t know whether the coin is head or tail. This is not the same as the coin being in the superposition of head and tail. This mean that the coin is actually in either the state $\vert 0 \rangle$ or $\vert 1 \rangle$; we just don’t know which one. Once we perform a transformation $H$ on the coin, the coin is in the superposition of head and tail. $$H\vert 0 \rangle= \frac{1}{\sqrt{2}}\left(\vert 0 \rangle + \vert 1 \rangle\right)$$ $$H\vert 1 \rangle= \frac{1}{\sqrt{2}}\left(\vert 0 \rangle - \vert 1 \rangle\right)$$ Although these two results look a bit different, if we perform a measurement with the basis of head and tail, we will get each result with probability $\frac{1}{2}$.
However, if the state of the coin is in $\frac{1}{\sqrt{2}}\left(\vert 0 \rangle + \vert 1 \rangle\right)$, and we perform $H$ on the coin, we will get the state $\vert 0 \rangle$ with probability 1.
$$H\frac{1}{\sqrt{2}}\left(\vert 0 \rangle + \vert 1 \rangle\right)= \vert 0 \rangle$$
 I hope this draw a clear distinction. The lack of knowledge about initial condition of a system is entirely different from superposition. We write something in a superposition state is exactly because it is in that superposition state not because we are ignorant about the initial condition.
I hope this draw a clear distinction. The lack of knowledge about initial condition of a system is entirely different from superposition. We write something in a superposition state is exactly because it is in that superposition state not because we are ignorant about the initial condition.
In a way, we can think of the superposition state as a state in its own right. The superposition state is as legit as the state of the coin being head or tail.
Conclusion
In this post, I have introduced the concept of wavefunctions. I have also illustrated the difference between wavefunctions and the lack of knowledge. I hope this post helps you understand the concept of wavefunctions better.
In the next post, I will introduce the concept of density operator; it is a wavefunction but on steroids.