Conversion between objects
I would like to begin this article with a question. Is there a way to turn bread into sugar? The answer from biology is yes. $$\textrm{Bread} \xrightarrow{\text{chewing}} \textrm{Smaller pieces of bread}$$ $$\textrm{Smaller pieces of bread} \xrightarrow{\text{enzyme}} \textrm{Sugar}$$
The question of whether or not there is a way is different from the question of whether or not the way is practical. A practicality question may ask whether or not a person can do this. The answer is still yes. A person can chew bread with their teeth and amylose in their saliva can break down the starch in the bread into disaccharide sugar. However, if we ask whether or not a tree can do this, the answer may be different. Obviously, a tree cannot chew bread. A tree might have another way to turn bread into sugar, but it is not the same way as a human does.
The difference between a person and a tree is more than a physical system. It’s also the different set of operations in which the agents, human and tree, can perform. A tree cannot chew while a human can. A human cannot photosynthesize while a tree can. Operations that an agent in a system can easily perform are called free operations.
The set of free operations is a key concept in resource theories. Following the set of free operations is a convertibility relation between the set of objects in the system. If there is a free operation that can turn object $a$ into object $b$, we say that $a$ can be converted into $b$ and write $a \rightarrow b$ or $a \succsim b$. The latter notion is a preorder relation. Mathematically, a preorder is a relation that is reflexive and transitive, meaning that if we can convert $a$ into $b$ and $b$ into $c$, we can convert $a$ into $c$. With the preorder relation, we can define a function $f$ which measures the value of the object. If $a \rightarrow b$, then $f(a) \geq f(b)$. This function is called a resource monotone. Intuitively, a resource monotone can be thought of as a function that tells the price of the object. For example, the price of a piece of bread is higher than the price of sugar.
Catalytic conversion
One of the interesting things about resource theories is the existence of a catalyst. It has the same concept as a catalyst in Chemistry. A catalyst is an object which allows previously unconvertible objects to be converted. For example, in the case of bread and sugar, a person cannot chew bread into sugar. But with the help of an enzyme, amylose, a person can convert bread into sugar. Even better, after such a process, the enzyme is still intact and can be used over and over again. However, the existence of a catalyst in a resource theory is not always the case. There’s an interesting sufficient condition that guarantees that a catalyst does not exist in a resource theory, and all can be found in a paper by Coecke, Fritz, and Spekkens. Even better, there is an analogy to the objects in the kitchen which can allow us to get the vibe of the concepts without appealing to the mathematical formalism.
Catalyst-free resource theories
We say that a resource theory has no catalyst or catalyst-free if any object that can be converted catalytically can be converted directly. $$a+c \rightarrow b+c \implies a \rightarrow b$$ This is a strong condition. It means that if we can convert a piece of bread into sugar with the help of a catalyst, we can convert a piece of bread into sugar without the catalyst. This is not always the case. As appeared in our example, a person cannot convert bread into sugar without the help of an enzyme.
Sufficient condition for catalyst-free resource theories
There are two conditions: quantity-like and non-interacting.
Quantity-like
The first condition is that the resource theory has a quantity-like structure. This means that if we have two objects $a$ and $b$ which are mutually convertible to one another, and both $a$ $b$ each are composed of two parts called $a_1$ and $a_2$ for $a$ and $b_1$ and $b_2$ for $b$. If $a_1$ can be converted to $b_1$ then $b_2$ must be able to be converted to $a_2$. Mathematically, if $a \rightarrow b$ and $b \rightarrow a$, then $a_1 \succsim b_1$ and $a_2 \succsim b_2$.
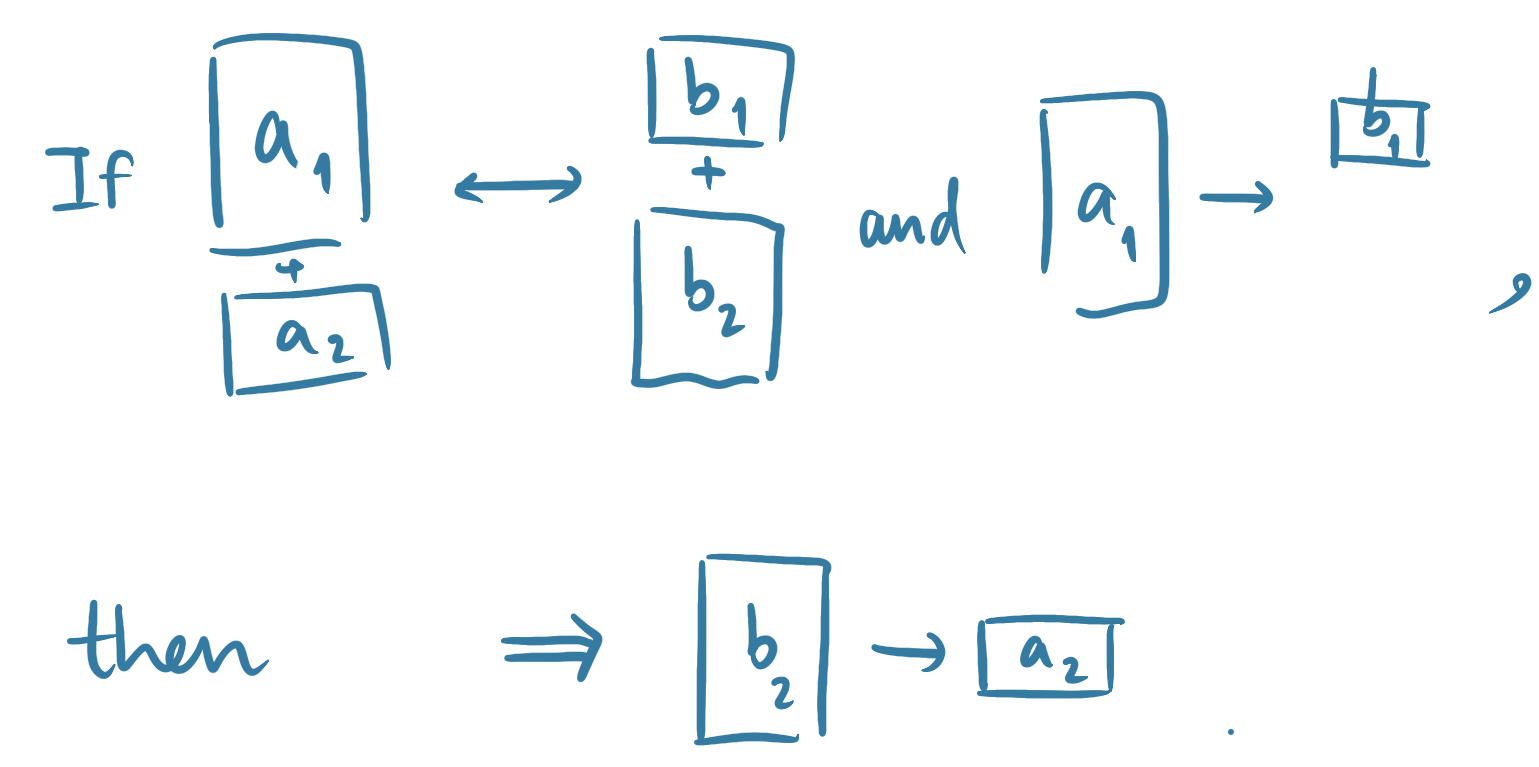
Analogously, in the kitchen, we can think of 2 equally-size loaves of bread. If we cut each loaf of bread into two pieces, and we find that one piece of the first loaf is larger than a piece of the second loaf, then the other piece of the second loaf must be larger than the other piece of the first loaf.
Non-interacting
The second condition is that the resource theory is non-interacting. This means that if we have two objects $a$ and $b = b_1 + b_2$ and $a\to b$, then we have that $a$ can be broken down into two parts one of which can be converted to $b_1$ and the other can be converted to $b_2$. Mathematically, if $a \rightarrow b$, then $\exists a_1, a_2$ such that $a = a_1 + a_2$, $a_1 \rightarrow b_1$ and $a_2 \rightarrow b_2$.
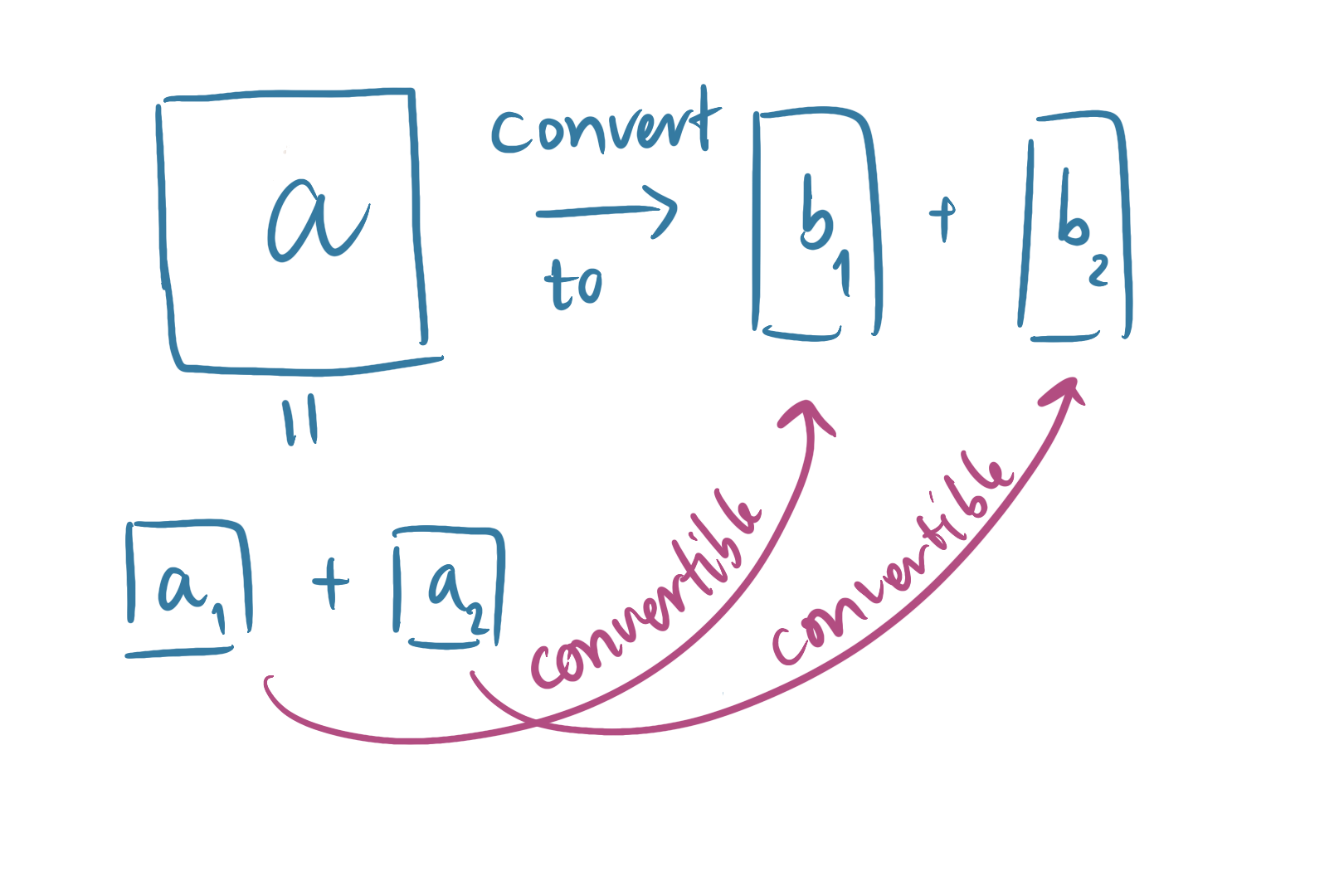 Analogously, in the kitchen, we can think of cutting a pizza. If we can convert a pizza into two servings. Then we can convert half of the pizza into one serving and the other half into the other serving.
Analogously, in the kitchen, we can think of cutting a pizza. If we can convert a pizza into two servings. Then we can convert half of the pizza into one serving and the other half into the other serving.
A sufficient condition for catalyst-free resource theories
If a resource theory satisfies both quantity-like and non-interacting conditions, then it is catalyst-free.
Proof Suppose that we have a resource theory that satisfies both quantity-like and non-interacting conditions. We want to show that it is catalyst-free. Suppose that we have two objects $a$ and $b$ such that $a+c \rightarrow b+c$. We want to show that $a \rightarrow b$. By the non-interacting condition, we have that $a + c = a_1 + a_2$ and $a_1 \rightarrow b$ and $a_2 \rightarrow c$. Since we have $a_2 \rightarrow c$, by being quantity we must also have $a \rightarrow a_1$. Therefore, we have that $a \rightarrow a_1$ and $a_1 \rightarrow b$. Therefore, we have that $a \rightarrow b$. $\blacksquare$
Conclusion
The convertibility problem is one of the problems in resource theories. With different physical settings, theories of resource convertibility can be different. In this article, I use a kitchen analogy to explain the concept of resource convertibility. I also show that despite the variety of resource theories, there is a sufficient condition that guarantees that a resource theory is catalyst-free. This condition is quantity-like and non-interacting.